Hi,

 

at

 

https://www.ibm.com/developerworks/community/forums/html/topic?id=e8342572-6dc5-4885-ae55-e154e8d37773&ps=25

 

 

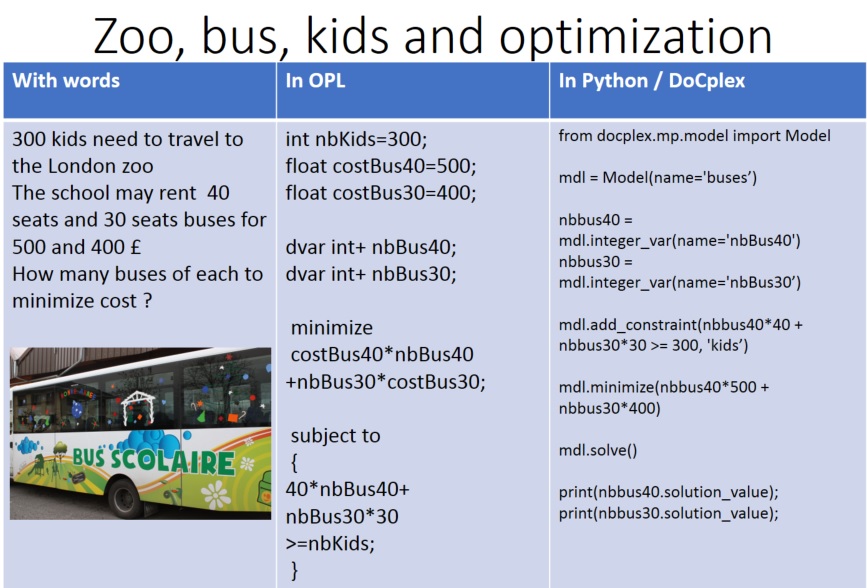
we handled what if analysis and dealt with many options with regards to the number of kids we need to bring to the zoo.

But now let's suppose all those options have some probabilities and we need to book buses the day before but in real time in the morning we may book some additional buses with an extra price. (+10%)

This is stochastic optimization. We want to minimize average cost. We call extra buses recourse variables.

In OPL, it is quite simple to move from a deterministic model to a stochastic model:

 

int nbKids=300;

{int} nbKidsScenarii={nbKids+i*10 | i in -10..2};
float proba[nbKidsScenarii]=[ 1, 1, 2, 2, 2 ,3 ,3 ,4,  5 ,10 ,50 ,10, 7];

assert sum(s in nbKidsScenarii) proba[s]==100; // total probability is 100

float costBus40=500;
float costBus30=400;

float costIncreaseIfLastMinute=1.1;

// number of buses booked in advance
dvar int+ nbBus40;
dvar int+ nbBus30;
// number of buses booked at the last minute which is far more expensive
// we call those recourse decision
dvar int+ nbBus40onTop[nbKidsScenarii] ;
dvar int+ nbBus30onTop[nbKidsScenarii] ;
 
minimize
 costBus40*nbBus40  +nbBus30*costBus30
 +
1/100*costIncreaseIfLastMinute*
sum(nbKids in nbKidsScenarii) proba[nbKids]*(costBus40*nbBus40onTop[nbKids]  +nbBus30onTop[nbKids]*costBus30);
 
subject to
{

 forall(nbKids in nbKidsScenarii)
   ctKids:40*(nbBus40+nbBus40onTop[nbKids])+(nbBus30+nbBus30onTop[nbKids])*30>=nbKids;
}

execute
{
writeln("nbBus40 = ",nbBus40);
writeln("nbBus30 = ",nbBus30);
writeln();
writeln("nbBus40 on top = ",nbBus40onTop);
writeln("nbBus30 on top = ",nbBus30onTop);
}

gives

 

// solution (optimal) with objective 3775.5
nbBus40 = 6
nbBus30 = 0

nbBus40 on top =  [0 0 0 0 0 0 0 0 1 0 0 1 2]
nbBus30 on top =  [0 0 0 0 0 1 1 1 0 2 2 1 0]

 

Note that if we do not use recourse variables then we hedge against the worst case:

 

dvar int+ nbBus40onTop[nbKidsScenarii] in 0..0;
dvar int+ nbBus30onTop[nbKidsScenarii] in 0..0;

will give

 

// solution (optimal) with objective 4000
nbBus40 = 8
nbBus30 = 0

nbBus40 on top =  [0 0 0 0 0 0 0 0 0 0 0 0 0]
nbBus30 on top =  [0 0 0 0 0 0 0 0 0 0 0 0 0]

 

which is more expensive (4000 vs 3775.5)

 

We should also compare the stochastic model with a naive approach : set the buses for the most probable scenario (300 kids) and then book extra buses

 

dvar int+ nbBus40 in 6..6;
dvar int+ nbBus30 in 2..2;

and then we get

// solution (optimal) with objective 3874.8

nbBus40 = 6
nbBus30 = 2

nbBus40 on top =  [0 0 0 0 0 0 0 0 0 0 0 0 0]
nbBus30 on top =  [0 0 0 0 0 0 0 0 0 0 0 1 1]

which is more expensive (3874.8 vs 3775.5)

 

 

So in a nutshell, stochastic optimization can save money and is quite easy in OPL.

 

regards

Alex Fleischer

PS:

Many how to with OPL at https://www.linkedin.com/pulse/how-opl-alex-fleischer/

Many examples from a very good book : https://www.linkedin.com/pulse/model-building-oplcplex-alex-fleischer/

Making optimization simple : https://www.linkedin.com/pulse/making-decision-optimization-simple-alex-fleischer/

#DecisionOptimization
#OPLusingCPLEXOptimizer

Originally posted by: Mohamed Awad

Hi Alex,

 

I would like to ask if this case can be extended to scheduling problems in case of using CP as solver.

 

Thanks in advance

Mohamed

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi,

have you had a look at the example in CPLEX_Studio129\opl\examples\opl\sched_stochastic_jobshop

?

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer

Originally posted by: Mohamed Awad

Hi Alex,

 

Yes I had a look on that example but it doesn't cover the case I am looking for as it is based on scenarios not distribution function. In your example, you added discrete probability distribution function so, I was asking if the same technique can be applied on scheduling problems. Let's consider the famous scheduling tutorial that comes with CPLEX. Could I change the task duration (masonry for example) to be based on discrete probability distribution instead of having a deterministic value.

 

Best regards

Mohamed 

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi

similar discussion at https://www.ibm.com/developerworks/community/forums/html/topic?id=8325d8a7-397f-46ce-ac51-2c250bbfb759&ps=25

CPLEX_Studio129\opl\examples\opl\sched_stochastic_jobshop

is with same probability for all scenarii.

If you want to have several proba you could add

float proba[Scns]=...;

in the .mod

and

proba=[1,10,20,3,5,10,2,3,4,5,5,2,3,4,1,1,1,1,19];

in the .dat

 

And then you can change

 

minimize sum(k in Scns) (max(j in Jobs) endOf(itvs[k][j][nbMchs-1])) / nbScns;

into

 

assert sum(k in Scns) proba[k]==100;

minimize 1/100*sum(k in Scns) proba[k]*(max(j in Jobs) endOf(itvs[k][j][nbMchs-1])) ;

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer

Originally posted by: Mohamed Awad

Hi Alex,

Thank you for your kind reply. I have few questions regarding the solution you sent. First, I would like to know what is the effect of changing the probabilities on the final schedule. If, for example, I increased the probability of a certain scenario, is its schedule will be the same as if its probability was kept small. Also, the final objective function is calculated by multiplying the probability of each scenario with its makespan. As I understand, the idea of stochastic optimization is to have different results based on each scenario while the idea of robust optimization is to have a single schedule that accommodates with different scenarios which makes it more conservative that stochastic optimization. So, in the solution you sent, what does having a single value for the objective function mean in the case of stochastic optimization. Finally, in the example of robust optimization you previously submitted, what kind of uncertainty set did you us.

Thanks in advance

Mohamed     

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi,

about " So, in the solution you sent, what does having a single value for the objective function mean in the case of stochastic optimization. "

The objective is the expected makespan

In the bus example the objective was the expected cost

In the robust bus example, the goal was to minimize cost taking into account a probabilistic constraint

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer