Hi,

at https://www.linkedin.com/pulse/solving-resource-constrained-project-scheduling-problems-laborie/

we can read an excellent post about RCPSP with CP Optimizer.

The python code there is simple but the OPL code that is in CPLEX_Studio129\opl\examples\opl\sched_rcpsp is quite simple too.

using CP;

int NbTasks = ...;
int NbRsrcs = ...;

range RsrcIds = 0..NbRsrcs-1;

int Capacity[r in RsrcIds] = ...;

tuple Task {
  key int id;
  int     pt;
  int     dmds[RsrcIds];
  {int}   succs;
}

{Task} Tasks = ...;

dvar interval itvs[t in Tasks]  size t.pt;

cumulFunction rsrcUsage[r in RsrcIds] =
  sum (t in Tasks: t.dmds[r]>0) pulse(itvs[t], t.dmds[r]);

 

minimize max(t in Tasks) endOf(itvs[t]);
subject to {
  forall (r in RsrcIds)
    rsrcUsage[r] <= Capacity[r];
  forall (t1 in Tasks, t2id in t1.succs)
    endBeforeStart(itvs[t1], itvs[<t2id>]);
}

execute {
  for (var t in Tasks) {
    writeln("Task " + t.id + " starts at " + itvs[t].start);
  }
}

and the .dat that would replace json

{
  
'ntasks'       : 6,
  
'nresources'   : 2,
  
'capacities'   : [ 2,3 ],
  
'durations'    : [ 2,4,1,1,1,2 ],
  
'requirements' : [ [ [0,1],[1,1],[2,2],[3,1],[4,1],[5,1] ],
                     [ [0,2],[1,1],[2,1],[3,1],[4,1],[5,2] ] ],
  
'successors'   : [ [0,2],[0,3],[2,4],[3,4],[3,5] ]
}

would be

NbTasks = 6;
NbRsrcs = 2;

Capacity = [ 2,3 ];

Tasks = {
 <0,2,[1,2],{2,3}>,
 <1,4,[1,1],{}>,
 <2,1,[2,1],{4}>,
 <3,1,[1,1],{4,5}>,
 <4,1,[1,1],{}>,
 <5,2,[1,2],{}>
 };

and in the IDE we immediately get

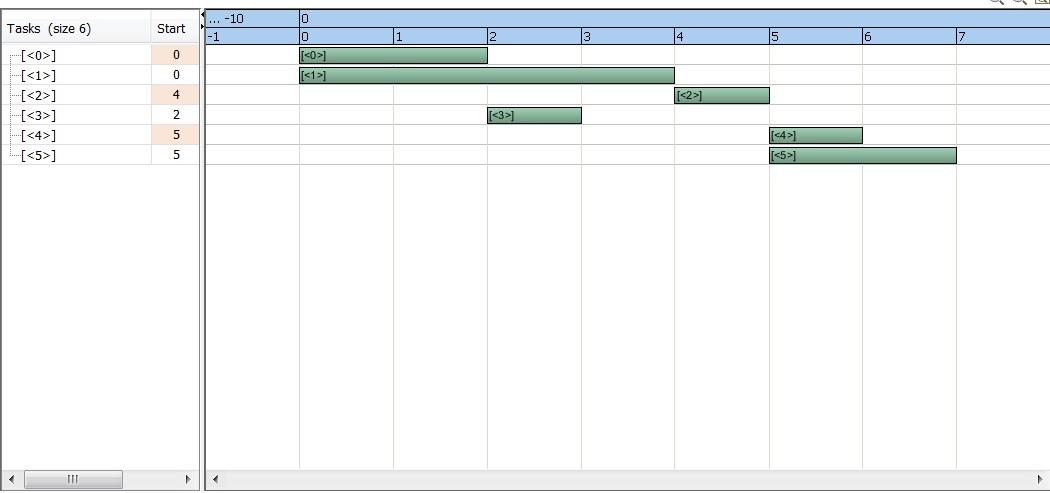
and

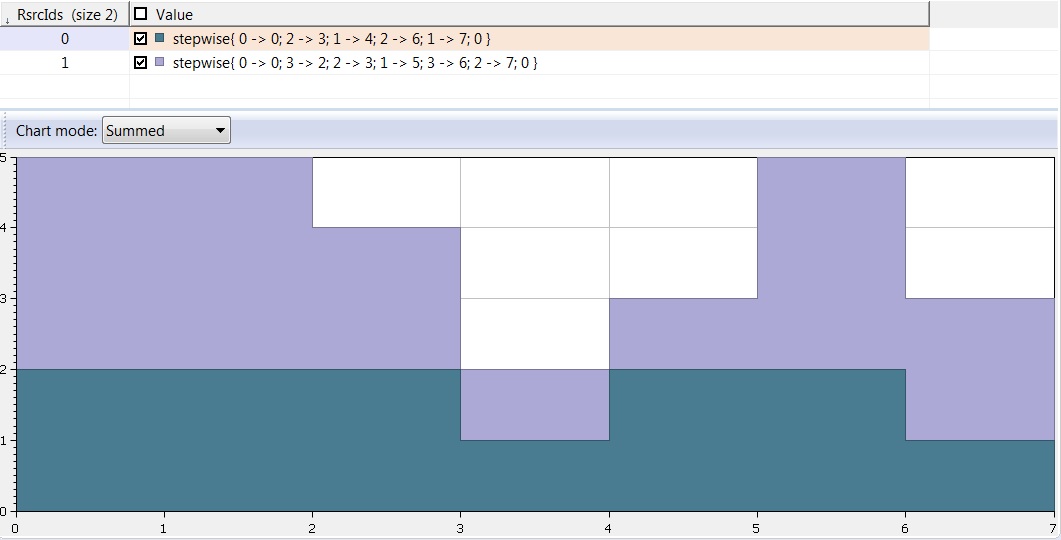
regards