Originally posted by: toonie

I want to write minimum spanning tree (MST) programming that I've already had the MST formulation (in MS word file: last page).

But i don't know how to write it's formulation in ILOG CPLEX :
This program want to find a link between each node. It has 2 constraints there are
1. connectivity constraint
2. no loop constraint

Decision variable (xij) is 0,1 >> 0 = no link and 1 = have a link between node i and j

I attached a MST formulation, MST model file (.mod) and MST data file (.dat) that i already write some.
#DecisionOptimization
#OPLusingCPLEXOptimizer

Originally posted by: Steve9

I have the same problem. I want to write the Minimum Spanning Tree in CPLEX language.

In attached word file is the objective as well as the restrictions.

The biggest challenge is to enter the restriction 'subtour elimination constraint'.

 

For the TSP we found this 'subtour elimination constraint' as an example in CPLEX:

forall(s in subtours)                       

   sum (i in S :  s.subtour[i] != 0)

      x[<minl(i, s.subtour[i]), maxl(i, s.subtour[i])>]

                   <=s.size-1;

 

If you use this restriction, cycles are part of the solution. But normally this should be avoided by the restriction.

 

Is here anybody who can help me out?

 

Many thanks in advance!

 

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi,

have you tried to have a look at the example in

opl\examples\opl\models\TravelingSalesmanProblem

?

There you ll find a way to remove cycles

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer

Originally posted by: Steve9

Hello Alex,

yes, I tried the one more often.

Unfortunately, everytime after solving the TSP example in CPLEX, there are still some cycles in (CPLEX is taking the data sheet with 17 cities).

Are you able to solve that one? Or do you maybe have another way to implement the 'SEC' restriction?

Many thanks in advance!

 

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi,

the TSP example does not produce any cycle:

In the .mod

if you add after

if (opl.newSubtourSize == opl.n) {

the following

var o=new IloOplOutputFile("result.txt");
          
          
          var kcity=opl.thisSubtour[1];
          for(var k=1;k<=opl.n;k++)
          {
              
              kcity=opl.thisSubtour[kcity];
              o.writeln(kcity);
              
                      
          }
          o.close();

then you ll get

13
7
8
6
17
14
15
3
11
10
2
5
9
12
16
1
4

 

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer

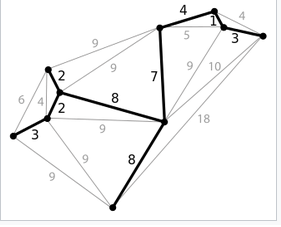
Let me give you a small example for the Minimum spanning tree out of https://en.wikipedia.org/wiki/Minimum_spanning_tree

 

.mod

tuple edge
{
    key int o;
    key int d;
    int weight;
}

{edge} edges=...;

{int} nodes={i.o | i in edges} union {i.d | i in edges};

range r=1..-2+ftoi(pow(2,card(nodes)));
{int} nodes2 [k in r] = {i | i in nodes: ((k div (ftoi(pow(2,(ord(nodes,i))))) mod 2) == 1)};

dvar boolean x[edges];

minimize sum (e in edges) x[e]*e.weight;
subject to
{
sum(e in edges) x[e]==card(nodes)-1;

// Subtour elimination constraints.
   
forall(k in r)  // all subsets but empty and all
    sum(e in edges:(e.o in nodes2[k]) && (e.d in nodes2[k])) x[e]<=card(nodes2[k])-1;  
   
}

{edge} solution={e | e in edges : x[e]==1};

execute
{
writeln("minimum spanning tree ",solution);
}

.dat

edges=
{
<1,2,9>,
<1,3,9>,
<1,4,8>,
<1,10,18>,
<2,3,3>,
<2,6,6>,
<3,4,9>,
<3,5,2>,
<3,6,2>,
<4,5,8>,
<4,7,7>,
<4,9,9>,
<4,10,10>,
<5,6,2>,
<5,7,9>,
<6,7,9>,
<7,8,4>,
<7,9,5>,
<8,9,1>,
<8,10,4>,
<9,10,3>,
};

which gives

minimum spanning tree  {<1 4 8> <2 3 3> <3 5 2> <4 5 8> <4 7 7> <5 6 2> <7 8 4>
     <8 9 1> <9 10 3>}

regards

 

regards

#DecisionOptimization

Originally posted by: Steve9

Hi Alex!

Thank you for your reply!

I need to work on the following formulation from Miller, Tucker and Zemlin in regard to the subtour elimination constraint:

 

The MTZ Formulation.

To exclude subtours, one can use extra variables
ui (i = 1, . . . , n), and the constraints

u1 = 1,
2 ≤ ui ≤ n ∀i     = 1,
ui − uj + 1 ≤ (n − 1)(1 − xij) ∀i     = 1, ∀j     = 1

 

How can I enter this into CPLEX?

Do you have any idea?

 

Many thanks in advance for yor help!

 

Best regards,

Steffen

 

#DecisionOptimization
#OPLusingCPLEXOptimizer

Hi,

let me show you with the example opl\examples\opl\models\TravelingSalesmanProblem

Let me rewrite the model with the MTZ (Miller-Tucker-Zemlin formulation) constraint to remove circuits:

// Cities
int     n       = ...;
range   Cities  = 1..n;

// Edges -- sparse set
tuple       edge        {int i; int j;}
setof(edge) Edges       = {<i,j> | ordered i,j in Cities};
int         dist[Edges] = ...;

setof(edge) Edges2       = {<i,j> | i,j in Cities : i!=j};
int         dist2[<i,j> in Edges2] = (<i,j> in Edges)?dist[<i,j>]:dist[<j,i>];

// Decision variables
dvar boolean x[Edges2];

dvar int u[1..n] in 1..n;

 

/*****************************************************************************
 *
 * MODEL
 *
 *****************************************************************************/

// Objective
minimize sum (<i,j> in Edges2) dist2[<i,j>]*x[<i,j>];
subject to {
   
   // Each city is linked with two other cities
   forall (j in Cities)
     {
        sum (<i,j> in Edges2) x[<i,j>]==1;
        sum (<j,k> in Edges2) x[<j,k>] == 1;
   }  
   
        
 // MTZ
 
u[1]==1;
forall(i in 2..n) 2<=u[i]<=n;
forall(e in Edges2:e.i!=1 && e.j!=1) (u[e.j]-u[e.i])+1<=(n-1)*(1-x[e]);
       
};

{edge} solution={e | e in Edges2 : x[e]==1};

execute
{
writeln("path ",solution);
}

 

.dat

 

n = 17;
dist = [
633
257
91
412
150
80
134
259
505
353
324
70
211
268
246
121
390
661
227
488
572
530
555
289
282
638
567
466
420
745
518
228
169
112
196
154
372
262
110
437
191
74
53
472
142
383
120
77
105
175
476
324
240
27
182
239
237
84
267
351
309
338
196
61
421
346
243
199
528
297
63
34
264
360
208
329
83
105
123
364
35
29
232
444
292
297
47
150
207
332
29
249
402
250
314
68
108
165
349
36
495
352
95
189
326
383
202
236
154
578
439
336
240
685
390
435
287
184
140
542
238
254
391
448
157
301
145
202
289
55
57
426
96
483
153
336
];

 

regards

#DecisionOptimization
#OPLusingCPLEXOptimizer

You may also find an example in http://caseine.org/pluginfile.php/2666/mod_resource/content/1/opl_tutorial.pdf

#DecisionOptimization
#OPLusingCPLEXOptimizer