PS:
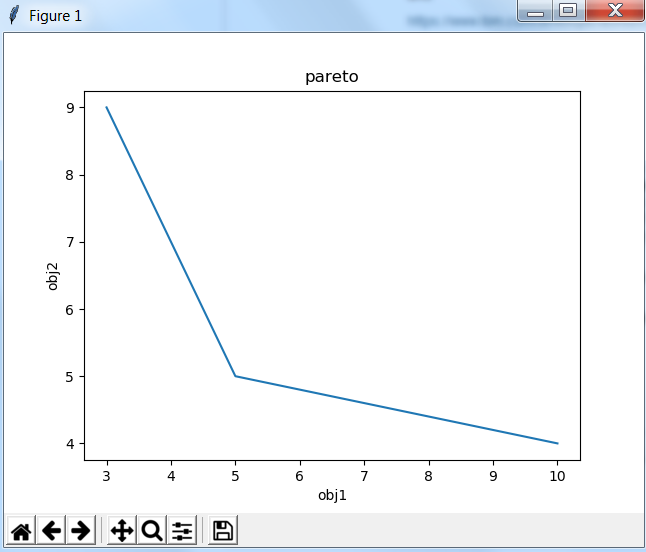
And then I got the question about showing the Pareto graph.
So let me share that too.
visu.mod
execute
{
// turn an OPL array into a python list
function getPythonListOfArray(_array)
{
var quote="\"";
var nextline="\\\n";
var res="[";
for(var i =1;i< _array.length;i++)
{
var value=_array[i];
if (typeof(value)=="string") res+=quote;
res+=value;
if (typeof(value)=="string") res+=quote;
res+=",";
res+=nextline;
}
res+="]";
return res;
}
// Display a function with points with x and y arrays of x and y
function displayXY(x,y,pythonpath,pythonfile,graphName,xName,yName)
{
writeln("displayXY ",x," ",y," ",pythonpath," ",pythonfile);
var python=new IloOplOutputFile(pythonfile);
python.writeln("import matplotlib.pyplot as plt");
python.writeln("x = ",getPythonListOfArray(x))
python.writeln("y = ",getPythonListOfArray(y))
python.writeln("plt.plot(x, y)");
python.writeln("plt.xlabel('",xName,"')");
python.writeln("plt.ylabel('",yName,"')");
python.writeln("plt.title('",graphName,"')");
python.writeln("plt.show()");
python.close();
IloOplExec(pythonpath+" "+ pythonfile,true);
}
}
and then
include "visu.mod";
int n=10;
int m=25;
range position = 1..n;
tuple t
{
int obj1;
int obj2;
}
sorted {t} nonDominatedSolutions;
dvar boolean x[position][position];
dvar int obj1 in position;
dvar int obj2 in position;
minimize obj1+obj2;
subject to
{
sum(i,j in position) x[i][j]==m;
obj1==max(i,j in position) i*x[i][j];
obj2==max(i,j in position) j*x[i][j];
}
execute
{
writeln("objectives : ",obj1," ",obj2);
writeln("-----------------------------");
writeln();
for(var i in position)
{
for(j in position) write((x[i][j]==1)?"+":" ");
writeln();
}
}
main
{
writeln("solution pools")
thisOplModel.generate();
cplex.solnpoolintensity=4;
cplex.solnpoolcapacity=1000;
cplex.solnpoolreplace=2;
cplex.populatelim=20000;
cplex.solve();
var nsolns = cplex.solnPoolNsolns;
writeln("n sol ",nsolns);
var obj1=new Array(nsolns);
var obj2=new Array(nsolns);;
for(var s = 0; s < nsolns; s++)
{
thisOplModel.setPoolSolution(s);
thisOplModel.postProcess();
obj1[s]=thisOplModel.obj1.solutionValue;
obj2[s]=thisOplModel.obj2.solutionValue;
}
writeln("not dominated solutions");
for(var s = 0; s < nsolns; s++)
for(var s2 = s+1; s2 < nsolns; s2++) if ((obj1[s]==obj1[s2]) && (obj2[s]==obj2[s2]))
{
obj1[s2]=thisOplModel.n+1;
obj2[s2]=thisOplModel.n+1;
}
for(var s = 0; s < nsolns; s++)
{
var dominated=0;
for(var s2 = 0; s2 < nsolns; s2++) if (s!=s2) if ((obj1[s2]<=obj1[s]) && (obj2[s2]<=obj2[s]))
dominated=1;
if (dominated==0)
{
thisOplModel.setPoolSolution(s);
thisOplModel.nonDominatedSolutions.add(obj1[s],obj2[s]);
thisOplModel.postProcess();
}
}
cplex.clearModel();
writeln(thisOplModel.nonDominatedSolutions);
var x2=new Array(thisOplModel.nonDominatedSolutions.size);
var y2=new Array(thisOplModel.nonDominatedSolutions.size);
for(var i=1;i<=thisOplModel.nonDominatedSolutions.size;i++)
{
x2[i]=Opl.item(thisOplModel.nonDominatedSolutions,i-1).obj1;
y2[i]=Opl.item(thisOplModel.nonDominatedSolutions,i-1).obj2;
}
var pythonpath="C:\\Users\\IBM_ADMIN\\AppData\\Local\\Programs\\Python\\Python36\\python.exe";
var pythonfile="C:\\displayXY.py";
displayXY(x2,y2,pythonpath,pythonfile,"pareto","obj1","obj2");
}
gives
regards
#DecisionOptimization