Method
The t-Distributed Stochastic Neighbor Embedding (t-SNE) technique is a non-linear dimensionality reduction method proposed by L.J.P. van der Maaten and G.E. Hinton in 2008. People typically use t-SNE for data visualization, but you can also use it for many other machine learning tasks like reducing the feature space and clustering, to mention a few. (You can learn more about the t-SNE method and its implementations in several programming languages here.)
In contrast to Principal Component Analysis (PCA), the most popular dimensionality reduction technique, t-SNE is better at capturing non-linear relationships in the data. PCA reduces the dimension of the feature space based on finding new vectors that maximize the linear variation of the data. Therefore, PCA can reduce the dimension of the data dramatically and without losing information when the linear correlations of the data are strong. (You don’t always need to choose between PCA or t-SNE since you can combine them and get the benefits of each technique. See an example here where PCA is used to reduce the feature space and t-SNE is used to visualize the PCA reduced space.)
The most important parameters of t-SNE:
- Perplexity — An educated guess about each point’s number of close neighbors. Helps to balance the local and global aspects of your data.
- Learning rate — By specifying how much to change the weights with each iteration, this value affects the speed of learning.
- Maximum Iterations — A cap on the number of iterations to perform.
Data
In this example, I used the MNIST database of handwritten digits, which you can download here. The database contains thousands of images of digits from 0 to 9, which researchers use to test their clustering and classification algorithms. The full data set consists on 60,000 images for training and 10,000 for testing, but to keep things simple for this example, I sample about 1,000 images per digit from the database, so a total of 10,000 images. Each row of the sample data set is a vectorized version of the original image (size 28 x 28 = 784) and a label for each image (zero, one, two, three, …, nine). Therefore, the dimension of the data set is 10,000 (images) by 785 (784 pixels plus a label).
What I learn while exploring t-SNE
Before writing this blog, I had never had the chance to learn about t-SNE. Every time that I needed to reduce the dimension of a feature space I would use PCA. I knew that PCA was great for reducing the dimension of data sets which columns are linearly correlated. Now I know that t-SNE is a viable alternative when the relationship of your columns is non-linear.
This is how the t-SNE grouping looks after several hundred iterations…
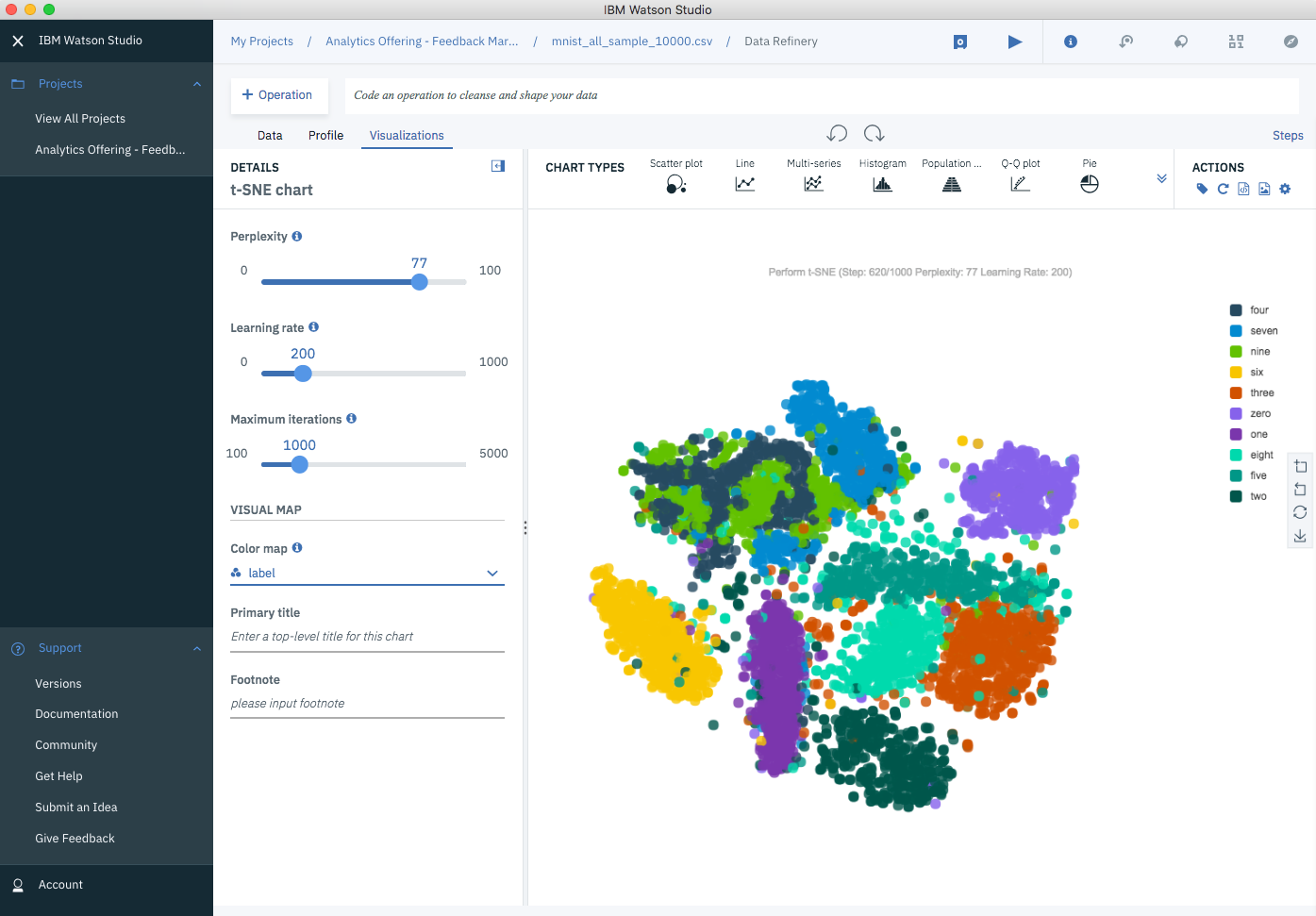 t-SNE on MNIST Data Set (at iterations 620)
t-SNE on MNIST Data Set (at iterations 620)
Step by step instructions on this github repo.
Find more about Watson Studio Desktop here or the Data Refinery here.
Jorge Castañón, Ph.D.
Senior Data Scientist @ Machine Learning Hub
--