Time Series Forecasting
A time series is a series of data points indexed (or listed or graphed) in time order. Time series forecasting is the use of a model to predict future values based on previously observed values. For example, you want to forecast the demand for a range of products and services to guide manufacturing and distribution.
Methods of modeling time series assume that history repeats itself—if not exactly, then closely enough that by studying the past, you can make better decisions in the future. To predict sales for next year, for example, you would probably start by looking at this year's sales and work backward to figure out what trends or patterns, if any, have developed in recent years. But patterns can be difficult to gauge. If your sales increase several weeks in a row, for example, is this part of a seasonal cycle or the beginning of a long-term trend?
Using statistical modeling techniques, you can analyze patterns in your past data and project those patterns to determine a range within which future values of the series are likely to fall, and get more accurate forecasts on which to make your decisions.
Here are two examples that time series forecast models will help.
Example 1: Each week that the market is open the Australian Wool Corporation set a floor price which determines their policy on intervention and is therefore a reflection of the overall price of wool for the week in question. Actual prices paid can depart considerably from the floor price. So, they want to get a more reasonable floor price for actual price from previous dataset(wool.csv) they have collected.
The dataset wool.csv consists of two columns “date” and “price”, which indicate the date variable (date) and weekly data of the log of the ratio between the price for fine grade wool and the floor price (wool). The time series are over a period of 309 weeks from 1976 through 1986. Sample data is shown below :

Example 2: An airport has found that in middle of the last few years, the number of passengers at the airport boomed significantly in a few months each year, and that required a large number of airport service personnel. The lack of forecasting ability lead to poor preparation for such a boom. The airport is hoping to forecast the number of passengers it may receive in the next 12 months, based on the number of passengers that have been collected in the last few decades.
The following chart is part of the raw data.

Recall that Exponential Smoothing is useful for forecasting series that exhibit trend and seasonality. Let’s try to perform the analysis by an Exponential Smoothing model.
IBM Exponential Smoothing Algorithm Introduction
The Exponential Smoothing (ES) model is a time series model for univariate time series. Thirteen types of exponential smoothing model are provided to handle level, trend, or seasonality in the time series.
- Trend: Whether data is increased or decreased with time. For the trend type, it can be one of No trend, Additive trend, Damped additive trend, Multiplicative trend and Polynomial.
- Seasonality: Whether the data changes meet certain time rules. For seasonal types, it can be one of No seasonality, Additive seasonality and Multiplicative seasonality.
An Exponential Smoothing model can be represented by notation (trend type, seasonal type). These supported trends and seasonalities are combined into 12 modeling methods, except for Polynomial Exponential. These types can be indicated by the settings.
IBM Exponential Smoothing Available in
Spark and Python API
Product Integration with UI
ES works in IBM SPSS modeler 18.1 and later; simply clicking on the icon will invoke it. The screenshot below displays the model types it can support:

Time Format Supporting
Besides standard time formats (such as Date, time and Timestamp, etc.), nonstandard time (such as a period format) is also supported by the IBM SPSS time series algorithm.
The Period format always looks like this:

The above data shows the noise value of two roads in one city. We can get two unique time series such as “(3,6,1), (3,6,2) …” and “(3,7,1), (3,7, 2) …” for each road.
Below we will show how ES can solve real business problems with 2 examples.
User Case 1
OK, let’s go back to the business problem we just mentioned. In this use case, we will forecast the “floor price” for the coming 12 weeks by methods of exponential smoothing.
But which combination of trend and seasonality is better among these 13 methods?
Trying them one by one? Or just pick one randomly and seeing how it works?
No, these are very inefficient practices. Let’s investigate our data more before we really start. Maybe, the data can tell us something important.
Raw Data Simple Analysis
First, let’s read this data and get a rough idea of its behavior, we can visually present the data by using TSE (Time Exploration Model), and then we can get the chart like below (X coordinate means time, Y coordinate means the wool price).

This chart shows the trend for “floor price” over time. The growth trend of the wool price is bigger and bigger over time, and seasonal changes which have a similar wave motion occurred accordingly. Maybe the seasons are delineated below:
So, let’s set the Exponential Smoothing method as “Additive Holt-Winters” in order to have a try since this method is appropriate for a series in which there is a linear trend and a seasonal effect that is constant over time.
Below I will give examples on how to run the SPSS Exponential Smoothing model in IBM SPSS Modeler and Watson Studio notebook separately.
Build Model And Forecast Using IBM SPSS Modeler
Build Winter’s Additive
In the Modeler UI “Build Options” tab of the Time Series node, “Winter’s additive” should be selected.
By clicking the “Run” button, we see that the stream execution was interrupted; the screenshot shows an error like the one below:

This shows that the data information we found from the raw data is not comprehensive and accurate and cannot fully reflect the true characteristics of the data. Modeling based on this is not accurate. Therefore, we should use the function of the algorithm itself to mine the true characteristics of the data as the standard for selecting a model.
From the error description above, the input has no seasonality and there are only 5 non-seasonal models that can be used as alternative models. They are:
- “simple exponential smoothing”,
- “Holt’s linear”,
- “Damped trend”,
- “multiplicative trend”,
- “Brown’s exponential smoothing”.
Combined with the data's increasing trend shown in the raw data exploration figure, we are left with “Holt’s linear” which data increases over time with no seasonal changes or the “multiplicative trend” method which is appropriate for a series in which there is a linear trend and a seasonal effect that changes with the magnitude of the series, so maybe it is appropriate. Let’s try to build them and select the most suitable one.
Model candidate 1: Holt’s Linear Method
Select as the Model type “Holt’s linear trend” in the Modeler UI and then build the model. We obtain the information below from this modeling:
1. Goodness-of-fit Statistics
After modeling, we got information Goodness-of-fit statistics of the model in the figure below. The Bayesian Information Criterion (BIC) and Akaike Information Criterion (AIC) values are very small, the R-Squared value is high at 0.982. All of these statistics show that this model is very nearly perfect.
2. ACF/PACF
From the histograms of ACF and PACF values shown in the below chart, we get that 95 percent of the inputs are useful for forecasting.

3.Forecasting
Since the input data interval is week, we suggest setting the forecast span at 12 (one quarter) in the modeling nugget (which is automatically generated once the modeling building is successful ) while doing forecasting.

4.Fit and Forecast Plot
The plot of the forecast results along with the raw data is shown below.
In the figure, The Y- coordinate is price value, X- coordinate is the time value. The curve for the price data is marked in blue; the curve of the model fit and forecast data are marked in red. The chart below is an enlarged view of the forecast:

From the image, the prediction data have a higher degree of fitting with the original data, and the forecast data trend is increasing. Next, let’s see the result when the model type is selected as “Multiplicative trend”.
Model candidate 2: Multiplicative Trend Method
1. Goodness-of-fit Statistics
After the model was built, we got the statistics for this model as shown below:

Comparing this with the “Holt’s liner” model type, we can see that the indicators of Goodness-of-fit statistics value, AIC, BIC and R-Squared values in this model type are worse.
2. ACF/PACF
From the histogram of ACF and PACF values listed in the chart below, we can see that 95 percent of inputs are useful for forecasting.

3.Forecasting
As with “Holt’s liner trend” method, the predicted span setting is 12 (one quarter). The raw and fit data forecast plot is shown below:
Let’s enlarge the forecast parts. The declining trend of the predicted data does not fit the overall trend of the raw data, so this may not be a good model for the user.
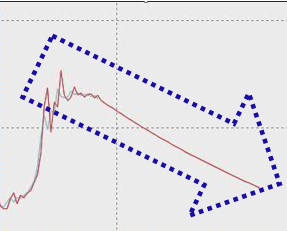
Based on the prediction results of these two models, the trend of the prediction results generated by the first model(Holt’s linear trend ) is consistent with the actual data trend, indicating that the predictive value of this model is highly reliable, it can give the user a more reliable and more reasonable “floor price”. In comparison, the model generated by “Holt’s liner trend” method is unreasonable for the inputs.
Using SPSS ES to Do Forecasting in Watson Studio
The following section shows how to invoke the SPSS ES model in a Watson Studio notebook using the kernel from Python3.5 with Spark 2.1 to build model and predict. Here we use the same input data autowool.csv as in the SPSS Modeler example above.
Based on the current product design, the input raw data must be processed by TSDP (Time Series Data Preparation, where the function includes Group, Aggregation/Distribution and Missing value handling) to obtain a suitable format for the ES model or other SPSS time series models to consume. Then RTSDP (Reverse Time Series Data Preparation) will convert the output(binary) from ES or other SPSS time series models to a readable format as raw data.
Unlike Watson Studio, SPSS Modeler and SPSS Statistics, are designed with TSDP and RTSDP embedded within the products and are transparent to user.
From the Notebook, upload the input data from "Find and add data", then click on input data as autowool.csv and select "Insert SparkSession DataFrame" from Insert to Code, then update the code to be like following in order to specify the input data schema.

The input data frame and the schema are shown as follows:
The following Python code shows how to build an ES model within the pipeline.

The following code shows how to run scoring to perform prediction:

We can see the prediction results below. Here we specify “setDeriveFutureIndicatorField(True)” in the code. It means that the output contains a flag field $FutureFlagwith value = 1 to show that the time is in the future. In the $TS-pricefield we can see the prediction. As “forecastSpan” is set as 7 in model building, we can predict prices 7 weeks into the future.


The sample notebook is available in the link below:
Notebook of ES user case1
User Case2
In this case, our goal is to predict the number of passengers that the airport may receive in the next 12 months. From the raw data, we know that:
- The number of passengers has increased more than three times in the recent ten years which indicates that the passenger number trend is additive.
- The number of passengers boomed during a certain time period each year which indicates that the passenger number changes seasonally.
So, we recommend that the “Winter’s additive” method to be used in modeling as it includes both an additive trend type and seasonality.
Build Model and Do Forecast by SPSS Modeler
Select the Model type as “Winter’s additive” in the Modeler UI and then build a model. We get the information below from the modeling.
1. Goodness-of-fit Statistics of modelling
After modeling, we obtained the Goodness-of-fit statistics in the figure below. The BIC, AIC and R-Squared (with a high value of 0.989) statistics show that this model is very close to perfect.

2. Forecasting
As with the “Winter’s additive” method, the predicted span setting is 12(one year).The raw and fit forecasting plot is shown below:
In the graph above, the red line is the score and predicted value, the blue line is raw data, the green line is the overall trend of the data.
Based on the overall trend and seasonal changes, the airport management knows that, with the booming tourism industry, more and more people choose to travel by plane, such that the number of passengers in the airport has increased exponentially over the years, and the number of people will suddenly increase from June to August each year, and following September the numbers will begin to decline, reaching a trough in November.
Let's zoom in on the predicted portion of the graph. They know the number of passengers will continue to grow in the next year and by July, the peak number of passengers they may receive is forecast to be 648.12, so they will need to prepare in advance to maintain their capability to provide good service.

Use SPSS ES to Do Forecasting in Watson Studio
We use the notebook of Scala2.11 with spark2.1 in this case.
From the Notebook, upload the input data from "Find and add data", then click on the input data airpass.csv and select "Insert SparkSession DataFrame" from Insert to Code, then update the code as follows to specify the input data schema.

The input data frame and the schema shows:

The following code shows how to build an ES model:
The following code shows how to predict the target:

We can see the prediction results below. Here, the output contains a flag field $FutureFlagwith a value of 1 in order to show that the time is in the future. In the $TS-airpassfield we can see the prediction. Since “forecastSpan” is set to 12 in model building, we can predict the number of passengers one year into the future.


The sample notebook is available in this link: Notebook of user case2
Reference:
Here are some links to help you understand trend and seasonality better.
#GlobalAIandDataScience#GlobalDataScience