Introduction

A fair dice is thrown several times till the sum of consecutive faces reaches 10 or above. Following questions are attempted to be answered.

1. What is the probability of reaching exact 10?
2. What is the expected number of throws to reach 10 or above?
3. What is the distribution of overshoot?
4. What is the distribution of the last face?

Background

The number of ways to have the sum total of s in n throws of a dice is the coefficient of x^s in (x + x² + x³ + x⁴ + x⁵ + x⁶)ⁿ = xⁿ (1 − x⁶ )ⁿ (1 − x)⁻ⁿ.

Following are the number of ways to reach a total of s in n throws.

Probability of Reaching Exact 10

Probability of getting an exact total of 10 is 3 × (1/6)² + 27 × (1/6)³ + 80 × (1/6)⁴ + 126 × (1/6)⁵ + 126 × (1/6)⁶ + 84 × (1/6)⁷ + 36 × (1/6)⁸ + 9 × (1/6)⁹ + 1 × (1/6)¹⁰ = 0.2892885

Expected Stop Time

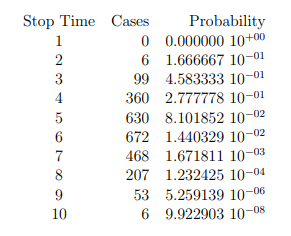
Expected Stop Time E(T) = 1 ×0×(1/6)¹ + 2×6×(1/6)² + 3×99× (1/6)³ + 4 × 360 × (1/6)⁴ + 5 × 630 × (1/6)⁵ + 6 × 672 × (1/6)⁶ + 7 × 468 × (1/6)⁷ + 8 × 207 × (1/6)⁸ + 9 × 53 × (1/6)⁹ + 10 × 6 × (1/6)¹⁰ = 3.323694 4

Distribution of Overshoot

Following table provides the distribution of overshoot when the total of the faces reaches 10 or above across various stop times.

Distribution of the Last Face

Following table provides the distribution of the last face before reaching a total of 10 or above across various stop times. 

Concluding Remarks

There is an interesting similarity between the distribution of overshoot and the distribution of last face. Let O(n, r) denote the number of ways overshoot r (0 ≤ r ≤ 5) can happen when stop time is n and L(n, r) denote the number of ways last face r (1 ≤ r ≤ 6) can happen when stop time is n. Then O(n, r) = L(n, 6 − r).

Let a(n, t) denote the number of ways to reach a total of t (1 ≤ t ≤ 15) in n throws. Then,

O(n, 0) = a(n − 1, 9) + a(n − 1, 8) + · · · + a(n − 1, 4)
L(n, 6) = a(n − 1, 4) + a(n − 1, 5) + · · · + a(n − 1, 9)

O(n, 1) = a(n − 1, 9) + a(n − 1, 8) + · · · + a(n − 1, 5)
L(n, 5) = a(n − 1, 5) + a(n − 1, 5) + · · · + a(n − 1, 9)
.
.
.
O(n, 5) = a(n − 1, 9)
L(n, 1) = a(n − 1, 9)

The argument settles the above mentioned feature of the distributions of overshoot and last face.

Published in Researchgate

QUESTION I: Suppose there are N balls, numbered from 1 to N, in an urn. One is picking up balls randomly one at a time with replacement and adding the numbers turning up. One can define a stop time when the sum reaches N or above. Above study could be carried out in this generalized set up.

QUESTION II: Imagine an administrator who wants to hire the best secretary out of n rank-able applicants for a position. The applicants are interviewed one by one in random order. A decision about each particular applicant is to be made immediately after the interview. Once rejected, an applicant cannot be recalled. During the interview, the administrator gains information sufficient to rank the applicant among all applicants interviewed so far, but is unaware of the quality of yet unseen applicants. The question is about the optimal strategy (stopping rule) to maximize the probability of selecting the best applicant.