“Graphs are a basic kind of data representation used in data science.” I recall writing that line on a whiteboard a few years ago during a course, to see what responses it might draw. I heard back a few “Well, is that really true?” remarks. By “graphs”, I don’t mean the sense of “graphics” and “diagrams”, rather the sense of organizing data as nodes and edges, with attribute values possible on either. Graphs were considered exotic circa 2014, and potentially quite expensive as a way of managing data – in other words, graph data was considered to be a game reserved for large tech companies. Big Data was in an earlier phase then, but machine learning use cases and the pace of innovation for hardware capabilities have both changed the ways we look at data. In a course taught today that statement on the whiteboard would be met with more nodding than grumbling.
Why Graphs Matter
To help describe the significance of graph data in real-world problems, consider that the world wide web itself is a graph and PageRank is a scalable graph algorithm.. There’s an interesting 2009 TED talk called “The Next Web” by Tim Berners-Lee (TBL). TBL is famous for his foundational role in the world wide web, URLs, HTTP, HTML, etc. In the video he describes motivations for creating the world wide web, citing his “frustration with unlocked potential” as they were working at CERN with documents spread across so many different servers. “Imagine if a link could to go to virtually any document?” Berners-Lee asked back in 1989 and the outcome made history. For so many things in the world, there are now unique names which start with “HTTP” and they link to other things with names that start with “HTTP” in other parts of the world. It’s safe to say that the potential of graph data continues to be realized thirty years later.
In his TED talk marking the 20th anniversary of WWW, Tim Berners-Lee made the case for linked data, i.e., graphs. There are some key points to consider. One idea is that data in general expresses not merely measurements but also relationships. Graphs are excellent for describing relationships between items – one can think of that as similar to the role that verbs (relations and transformations) have in language when compared with nouns (things). It’s convenient that graphs are very effective for accumulating results from many people who are collecting and curating data in parallel. DBpedia provides a good example of the power of graphs in the process of parallel curation, with its structured content extracted from the pages in Wikipedia, a crowd-sourced online resource which is continually growing. Take a look at the entry for Artificial Neural Networks to see its properties and how it links to related terms – compared with the associated Wikipedia page. If Wikipedia is analogous to expressing the properties of the noun in the above relationship, then DBpedia harnesses both noun and verb and is therefore more expressive.
TBL alludes to another subtle, important point in the video: data which is structured as a graph can represent more information than a comparable amount of data stored as documents, or even as tables. Wikipedia, WordNet, Thesaurus.com – these are large graphs that lead to the more general notion of a knowledge graph. That’s often referred to as ontology work. For example, the US Library of Congress (LOC) publishes a set of linked data services for subject headings, company names, and other classification systems used in its overall catalog. See the neural networks entry in LOC for a comparison with the DBpedia/Wikipedia information linked above. Both DBpedia and Library of Congress expose data using a graph language called SKOS (Simple Knowledge Organization System), which is based atop a popular and more formal ontology language called OWL (W3C Web Ontology Language). LOC and DBpedia offer ontology APIs, at least for more general (“upper ontology”) concepts. To TBL’s point, these data sources offered as disparate API’s, meaning outside of an ontology, would lack the relational information that they inherently offer when stored as a graph.
Comparing Graphs: RDBMS, Frameworks, Hardware
How do graphs compare with more traditional and well known data structures? The subject of relations in data has a long and storied past, dating back to Edgar Codd’s work at IBM Research. In 1970 Codd published “A Relational Model of Data for Large Shared Data Banks”, which led to relational databases and SQL. However, RDBMS stores are not effective for representing graphs. For example when you find SQL queries which have many self-joins, that’s typically an anti-pattern indicating that the data could be represented more efficiently as a graph.
This is a good point to mention a favorite essay, “On Graph Computing” by Marko Rodriguez. Marko is the author of the open source Apache TinkerPop and contributor on related graph tools. That essay introduces important concepts in graph computing, such as traversals, adjacency list, cycles, degree, as well as some of the performance issues encountered in distributed systems for graph computation.
In terms of open source frameworks for managing graph data, there’s quite a range of different options. I’ve worked with GraphX which runs atop Apache Spark. Neo4j has a popular Python library. TigerGraph is another framework that’s gained substantial traction for data science work in recent years.
To be candid, I’m not entirely convinced about the support for graph algorithms found in any particular graph database framework. Generally the large-scale distributed graph frameworks are aimed at solving data engineering problems instead of enabling advanced algorithms. The frameworks tend to emphasize relatively simple queries, i.e., traversals, which then result in smaller subgraphs. Those subgraphs can be moved into memory for more advanced algorithms work using other libraries. That’s probably a reasonable trade-off.
The fact is that hardware has been evolving rapidly: multicore processors and large memory spaces allow for substantial graphs – and complex graph algorithms – to be run entirely in memory. For example, ten years ago I was working on one of the early large-scale deployments of Apache Hadoop in the cloud. That project was written in Java, with a distributed machine learning algorithm running on 100x large servers. Last year I tried running the same data rates, and the same algorithm but this time rewritten in Python – it now runs faster on my laptop than it did a decade ago on an entire cluster. Hardware has changed significantly.
For working with in-memory graph data in Python, NetworkX is my favorite library. It’s simple, fast, and effective. Here’s an example where we take a Krackhardt kite graph and calculate measures for centrality for each node. In other words, which nodes are most “important” within the graph?
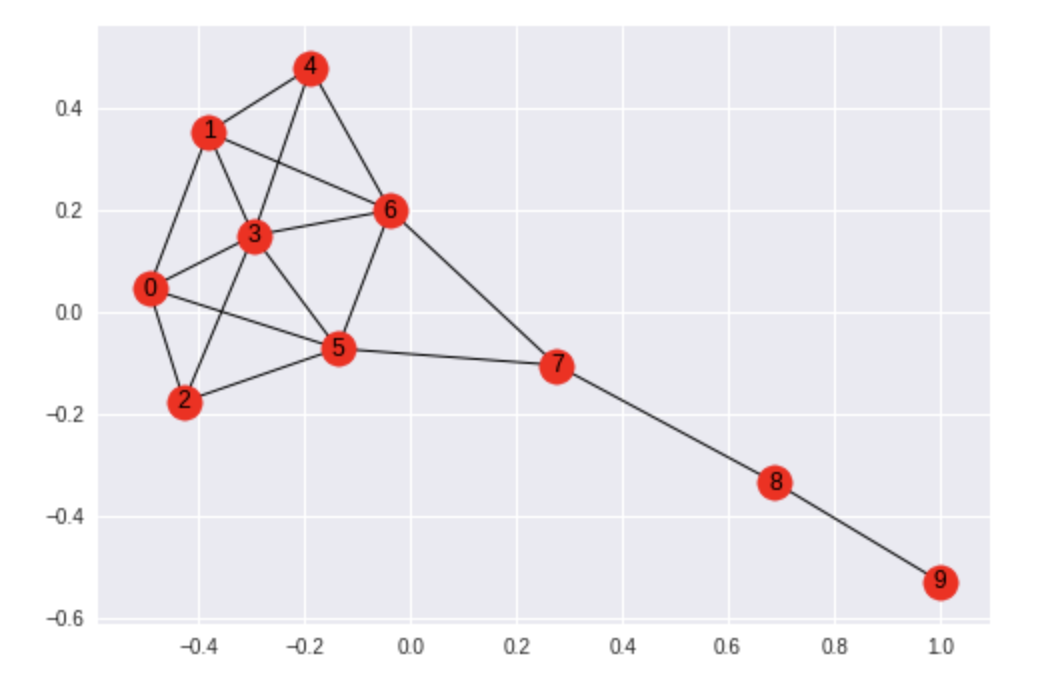
We know from graph theory that nodes 5 and 6 will have the highest centrality measures, and NetworkX makes this simple to calculate in Python:
import networkx as nx
G = nx.krackhardt_kite_graph()
c = nx.closeness_centrality(G)
results = [[v, round(c[v], 3)] for v in G.nodes()]
sorted(results, key=lambda x: x[1], reverse=True)
As expected, nodes 5 and 6 rank the highest, while node 9 ranks the lowest – the node at the “tail end” of the kite:
[[5, 0.643],
[6, 0.643],
[3, 0.6],
[7, 0.6],
[0, 0.529],
[1, 0.529],
[2, 0.5],
[4, 0.5],
[8, 0.429],
[9, 0.31]]
Imagine if those nodes represented vendors in a supply chain graph, or influencers in a social graph, then would centrality seem intuitive answering “Which nodes are most connected?” within the data? For the code, see the krackhardt_centrality.ipynb notebook on GitHub.
Graph Algorithms
You may wonder about “Graph algorithms: What’s possible?” To start, we should cover a bit about algebraic graph theory. The gist for much of that theory is that graphs translate into matrices. Matrices allow us to apply linear algebra. Since we already have great libraries and hardware support for efficient linear algebra work, that approach works well. For example you’ll see mention of using an adjacency matrix where each node in a graph has its own row and column in a matrix, with a 1 value for each row/column element representing a pair of connected nodes and a 0 value otherwise. Linear operations on an adjacency matrix can accomplish much the same work as graph traversals, but they can also be easily parallelized.
One of the cornerstones of linear algebra work on large-scale data is to leverage eigenvalues and eigenvectors, and you’ll see these used often with graph algorithms. Generally it’s much more efficient to convert the graph data into an adjacency matrix, find the principal eigenvector for that matrix, then apply a power method using the principal eigenvector. As an example of this PageRank can be calculated by iterating through a graph, although that becomes expensive at scale. If most of the matrix elements will be zero anyway (translated: most web pages link to only a few other web pages) linear algebra can gain us significant efficiencies in parallel processing. Note: PageRank is a special case of a more general graph algorithm called eigenvalue centrality.
Applications
Social networks and communities are another area where graph computing is so essential. One of my favorite examples is in the paper “From Amateurs to Connoisseurs: Modeling the Evolution of User Expertise through Online Reviews” by Julian McAuley and Jure Leskovec at Stanford. While the paper mentions the word “graph” only once, working with very large-scale graphs is an area of expertise for Professor Leskovec. Then post-doc McAuley applied their team’s algorithms research on data from the RateBeer social network, describing how as an Australian he felt thoroughly perplexed by American preferences for beer and needed to research the matter. Ratings and recommendation systems, such as RateBeer, generally use graphs where there are links between users and items – in this case between people who rate beers and the beers they like or dislike. I got to catch a lecture where this paper was presented, and some of McAuley’s conclusions are both insightful and hilarious. Here’s one of the key illustrations from the paper:
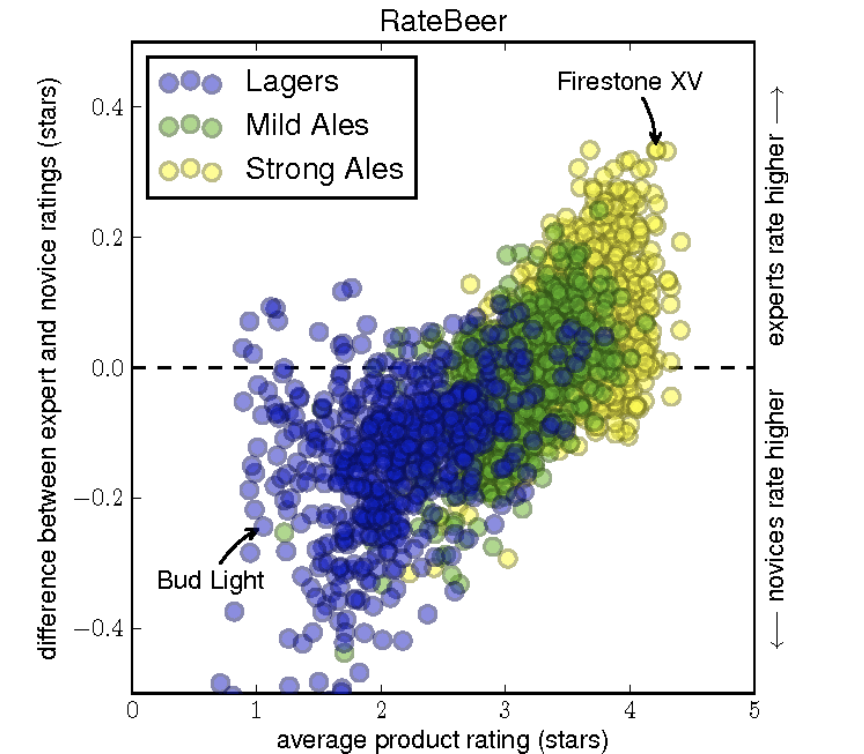
Interestingly, McAuley and Leskovec were able to demonstrate how they could detect levels of expertise and whether a person was likely to leave a community soon based on their use of language relative to the community in general. That could be useful in many industry use cases.
Another great example of data science work with graph data is in the article “Vast set of public CVs reveals the world’s most migratory scientists” by John Bohannon in Science magazine. Bohannon – who’s now a researcher at Primer AI in SF – used data from ORCID listings of research works to study “migratory” patterns among scientists. The article goes on to describe various ways that graph data can be leveraged:
As ORCID grows into a more comprehensive sample, policymakers will likely use it to track the impact of their efforts to entice research talent. Meanwhile, the data offer a unique glimpse into the migratory lives of the world’s knowledge producers.
Graph processing is also an integral part of human language. We make graph-like references to concepts as we speak or write. WordNet is a large, computable thesaurus which provides a graph of hypernyms and hyponyms. In other words, the entry for the word cat is linked to a parent class feline and a subclass kitten – providing graph traversals from any noun out to more general (hypernym) or more specific (hyponym) categories. WordNet represents an ontology for the English language. There are implementations for many other languages now as well.
In the 2004 paper, “TextRank: Bringing Order into Texts”, Rada Mihalcea and Paul Tarau introduced a way to leverage the graph-like aspects of writing for natural language processing (NLP). After parsing a raw text, splitting it into sentences, and tagging each word for its “part of speech” (noun, verb, adjective, etc.), TextRank constructs a graph from that text. By linking together neighboring nouns and verbs, and also linking together repeated instances of the same word within a text, the graph represents contexts parsed from the text. Here’s an example graph examined in the paper:

Running an algorithm similar to PageRank on the graph then produces the top-ranked noun phrases from the text. Note that TextRank doesn’t need to understand the individual words to create its summarization of a text. The paper showed comparable performance with human annotations (i.e., science editors) for summaries of scientific papers. If you’d like to try it, I wrote open source implementations in Java on Hadoop, Scala on Spark, and more recently PyTextRank which is in Python using spaCy and NetworkX.
Going a few steps further, consider how the output from TextRank is a graph of concepts. If you have many documents concerning a set of related topics, TextRank is one way to begin constructing a knowledge graph from those documents. Moreover, if you already have a knowledge graph about topics related to the texts you’re parsing, then you can:
- Transfer relations from the prior knowledge graph to the TextRank-generated graph to make it converge faster and produce better results.
- Use the TextRank results to augment your knowledge graph.
Initially I used WordNet hypernyms and hyponyms to augment graphs for TextRank as a way to accelerate it. More recently I’ve begun working with customized knowledge graphs to augment the graphs used in TextRank. This is effectively a form of transfer learning applied to NLP.
Advanced Graphs
Looking into large knowledge graphs and some of the more advanced kinds of graph algorithms which can be used on them… One of the more interesting areas of research is in topological data analysis (TDA). Imagine being able to zoom in or out of a large graph, like a “fly by” visualization, so that you could examine either its details or its overall structure. Alternatively, consider the detail shown of photos from a low-flying drone, from a jet airliner, or from the International Space Station. The trick is to preserve the “shape” of that data as you zoom in or out. The mathematics for that “zoom” feature is called persistent homology and it can be super useful. However, there are a few caveats. First, the math involved is complex. Second, the computation required had been quite expensive – at least until recently. If you’d like to look at the math, the paper “Topological Data Analysis of Biological Aggregation Models” gives a good introduction. One of the paper’s authors, Chad Topaz, wrote a much more approachable and entertaining tutorial about homology. Also, in terms of the computation required it turns out that GPUs can be used for TDA. That presents a game-changer, much like how GPUs revolutionized the costs of deep learning.
As in other areas of Big Data, often the goal with graphs is to find low-dimensional representations for higher-dimensional data. Another way to think of that is “What if you could separate a large data set into a few interesting details versus a whole bunch of non-interesting background?” Then filter out the background. Seems like a good approach for the perennial “needle in a haystack” problems we face with Big Data – if you can represent the data as a graph. There are a few platforms emerging to leverage TDA, such as DataRefiner.
There’s also a simpler way. Suppose you’re using machine learning to construct large-scale graphs from your data. When you’re working with large complex graphs many of the “traditional” graph algorithms come from common use cases such social networks. Those tend to filter the nodes of a graph, based on metrics such as degree and centrality which can be readily computed. For example, there’s the strongly connected components algorithm which yields a vague approximation of TDA. Less important nodes in a graph will tend to have fewer connections, so delete those first and the resulting subgraph will retain a similar shape. However that can lead to significant distortions of the data.
The 2009 paper “Extracting the multiscale backbone of complex weighted networks” by M. Ángeles Serrano, Marían Boguñá, and Alessandro Vespignani considered how to filter the edges of a graph instead. The “multiscale backbone” part of its approach is akin to the “zoom” aspects of TDA, and provide a graph algorithm called a disparity filter. If you’d like to work with that, I’ve written an open source Python implementation called disparity filter, based on NetworkX. For example, suppose you construct a large knowledge graph from your data, then apply a disparity filter so that you can analyze the top few nodes and their relationships – instead of having to look through thousands of nodes and their tangle of relationships all at once.
Machine learning with graphs is an area that’s been exploding. One good example is node2vec which also comes from Jure Leskovec’s group at Stanford. That learns low-dimensional representations for the nodes in a graph. Another example, more recently, is “Interpretable Graph Convolutional Neural Networks for Inference on Noisy Knowledge Graph” by researchers at BenevolentAI. Translated: they use deep learning to learn biomedical knowledge graphs and make predictions, such was which new drugs might fight particular diseases. While we’re on the topic, admittedly I haven’t covered much about use cases for graph data in life sciences. Those are myriad. Genomic research in particular relies heavily` on graph analysis, graph databases, ontology, etc. That’s probably a good subject for another article.
One last item about graph data: while it’s possible to “shoe horn” a graph into a matrix, then apply algebraic graph theory, that approximate is less than ideal. Real-world graphs tend to have multiple attributes per edge, which is important for applications. Mathematically that case requires the use of tensors plus complicated techniques such as tensor decomposition. By the mid-2010s, some advances in math made tensor operations more tractable within open source frameworks, and that coincided with an important use case: the large-scale graphs used to train neural networks for deep learning. You may have heard of one such graph processing framework called TensorFlow. That’s a topic for another day.
Summary
If you find that graphs, graph data, graph theory, graph algorithms, graph computation, etc., are really interesting and you want to read more papers and leading-edge research, then I highly recommend following David Gleich at Purdue. He’s done fascinating work with algorithms such as PageRank, plus how to leverage advanced math for Big Data on open source frameworks. I’ve caught a few of his lectures and they’re outstanding. There’s also the SparseSuite Matrix Collection by Tim Davis at Texas A&M – the only time I’ve ever seen standing-room only for a Stanford math lecture!
Also, there are many interesting conferences each year related to these topics, although I’m watching two especially – which will have great content about working with knowledge graphs:
For conferences related to data science in general, see https://derwen.ai/watchlist which we curate – and are eager to get suggested additions.
See you on the forums!
To try graphs theory yourself, try a Watson Studio Desktop Trial >>
PS: many thanks to @William Roberts for editing and valuable contributions to this article.
#Article#GlobalAIandDataScience#GlobalDataScience#MachineLearning#Python#TransferLearning