Global AI and Data Science

Hello awesome IBM community,

Previously we had talked about Hilbert spaces, a complex vector space where quantum states reside. The dimension of H corresponds to the number of basis states. For a single qubit, H is two-dimensional. For$n$ qubits, $\mathcal{H}$ is 2ⁿ-dimensional, spanned by basis states |0⟩ and |1⟩.
We can represent these basis states as column vectors: 

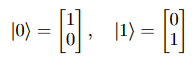
Each arrow represents the action of a unitary gate, transitioning between basis states.

Unitary Evolution

Unitary transformations describe how quantum states evolve over time. Mathematically, a unitary operator U acts on a quantum state |ψ⟩ as follows:
|ψ′⟩ = U|ψ⟩. In matrix form, U is a unitary matrix, meaning that U^†U = I, where U^† is the adjoint (conjugate transpose) of U, and I is the identity matrix.

For a single-qubit unitary, we have,

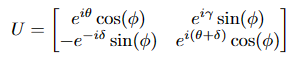
let’s break down the components of this matrix and explain their meanings:

1. e^iθ cos(φ): This component in the top-left corner of the matrix corresponds to the amplitude and phase change of the quantum state’s |0⟩ basis state:
          • cos(φ): This represents the amplitude (or probability) of transitioning to the |0⟩ state.
          • e^iθ : This introduces a phase factor to the |0⟩ state. The phase is determined by the angle θ. This phase factor can be used to perform various quantum operations.
2. e^iγ sin(φ): This component in the top-right corner of the matrix corresponds to the amplitude and phase change of the quantum state’s |1⟩ basis state:
         • sin(φ): This represents the amplitude (or probability) of transitioning to the |1⟩ state.
         • e^iγ : Similar to the previous component, this introduces a phase factor to the |1⟩ state. The phase is determined by the angle γ. Like before, this phase factor can be used for quantum operations.
3. −e^−iδ sin(φ): This component in the bottom-left corner of the matrix is the negative amplitude and phase change for the |0⟩ basis state:
         • − sin(φ): This represents the negative amplitude (or probability) of transitioning to the |0⟩ state.
         • −e^−iδ : This introduces a phase factor with a negative sign to the |0⟩ state. The phase is determined by the angle δ.
4. e^i(θ+δ) cos(φ): This component in the bottom-right corner of the matrix is the amplitude and phase change for the |1⟩ basis state:
         • cos(φ): This represents the amplitude (or probability) of transitioning to the |1⟩ state.
         • e^i(θ+δ): This introduces a phase factor to the |1⟩ state. The phase is determined by the sum of angles θ and δ.

This unitary transformation matrix U represents a quantum gate or operation that can be applied to a quantum state, and it determines how the amplitudes and phases of the basis states |0⟩ and |1⟩ are modified. The specific values of the angles θ, φ, γ, and δ will determine the exact nature of the quantum operation or gate being performed.

Measurement

When we measure a quantum state, it collapses probabilistically to one of the basis states. The probability of measuring a state |ψ⟩ in basis state |b⟩ is given by the Born rule: P(b) = |⟨b|ψ⟩|². Here, ⟨b|ψ⟩ represents the inner product (scalar product) between |b⟩ and |ψ⟩.

For example, if we measure a qubit in the |0⟩ state, the probability is |⟨0|ψ⟩|².

It illustrates the transformation of a quantum state through two steps: the Hadamard gate (H) and a measurement (M).

1. |0⟩: This is the initial quantum state, often referred to as the "ground state" or "ket 0". It represents a qubit in the |0⟩ state.
2. Hadamard Gate (H): The symbol "H" represents the Hadamard gate, which is a quantum gate used to create superposition. When applied to a qubit in the |0⟩ state, it transforms the state into a superposition of |0⟩ and |1⟩ with equal probabilities: 1/√2 (|0⟩ + |1⟩). Where the qubit is simultaneously in both |0⟩ and |1⟩ states with a probability amplitude of 1/√2 for each.
3. Measurement (M): The symbol "M" represents a measurement operation. In quantum mechanics, when we measure a quantum state, it collapses probabilistically to one of its basis states (in this case, |0⟩ or |1⟩) based on the Born rule. The Born rule states that the probability of measuring a state in a specific basis state is equal to the square of the absolute value of the probability amplitude for that basis state.
4. Outcome: |0⟩ with 1/2 probability: The diagram shows that when we measure the superposition state created by the Hadamard gate, there is a 1/2 probability of obtaining the outcome |0⟩. This means that upon measurement, the qubit will either collapse to |0⟩ or |1⟩ with equal chances. The outcome is probabilistic.

Quantum systems are known for their ability to evolve over time in a peculiar and deterministic manner. This evolution is governed by unitary transformations, represented by unitary matrices within a mathematical space known as a Hilbert space. These transformations are the backbone of quantum gates and algorithms, enabling quantum computers to perform complex computations beyond the reach of classical computers. When a quantum system is measured, its state undergoes a profound transformation. Unlike classical systems, where measurements yield precise outcomes, quantum measurements are probabilistic. The outcome depends on the inner product (or scalar product) between the quantum state and the basis states.

This  phenomenon is encapsulated in the Born rule, which gives us the probabilities associated with various measurement outcomes. These fundamental concepts lay the groundwork for quantum algorithms, quantum design, and the development of practical quantum applications.

Quantum computing is an ever-evolving field, and there's always more to learn and explore. Any questions, insights, and perspectives are valuable contributions to our collective understanding. Thanks for the attention.

Kind regards.