One of my peer offering managers recently
tweeted about a nice
tutorial of pulling crypto currency statistics. As a fan of Bitcoin, Etherium, and the other cryptos, I decided to pull the dataset into
SPSS Statistics 25 to explore the data myself. In doing so, I used some of the new
features of 25 including the new Chart builder capabilities and Bayesian statistics and reminded myself of a cool insight.
[caption id="attachment_7011" align="alignnone" width="3437"]
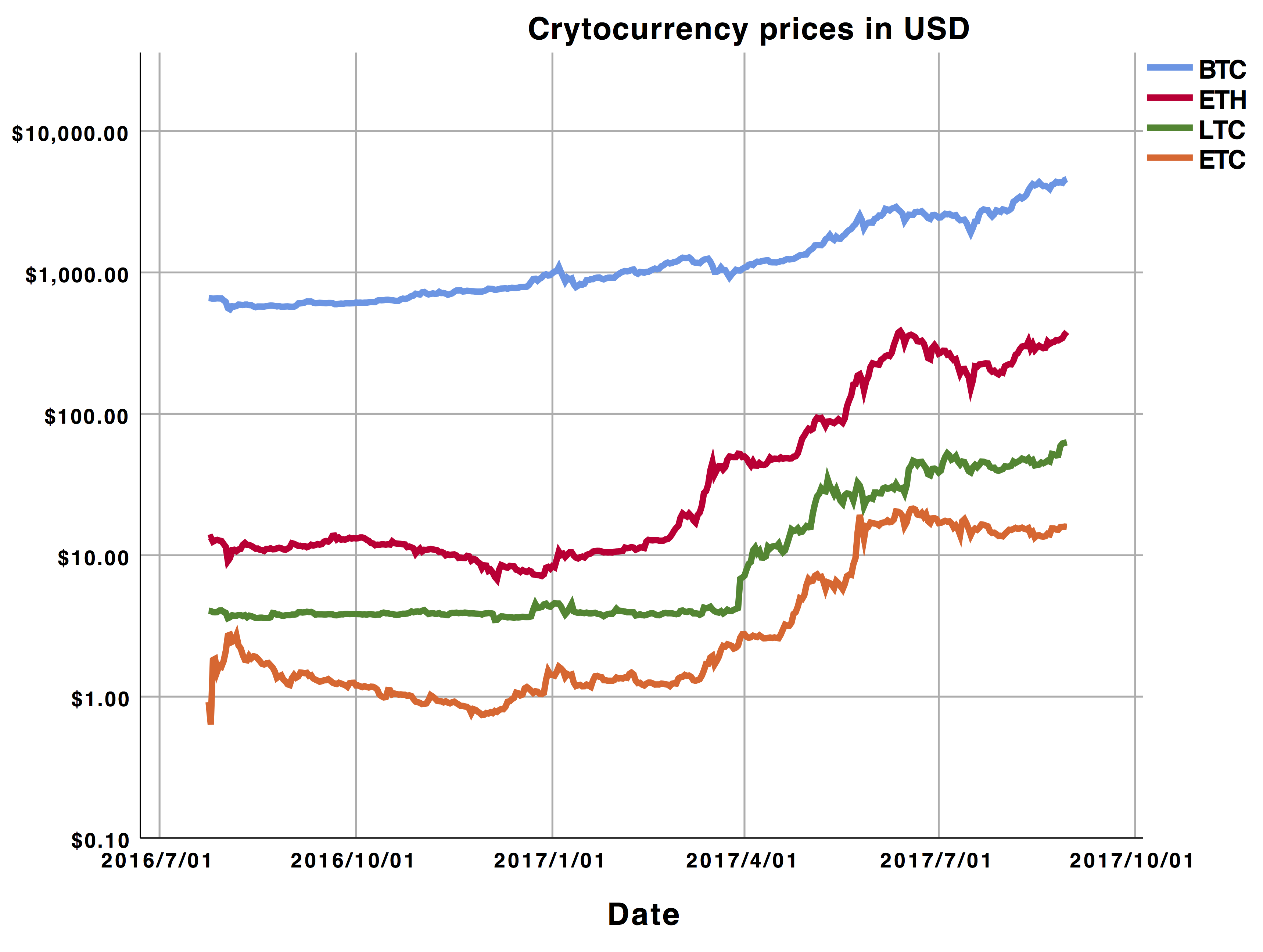
[/caption]
First, I pulled the crypto prices for all of 2016 and 2017 in to SPSS Statistics 25 and graphed the pairwise scatter plots of these prices per year:
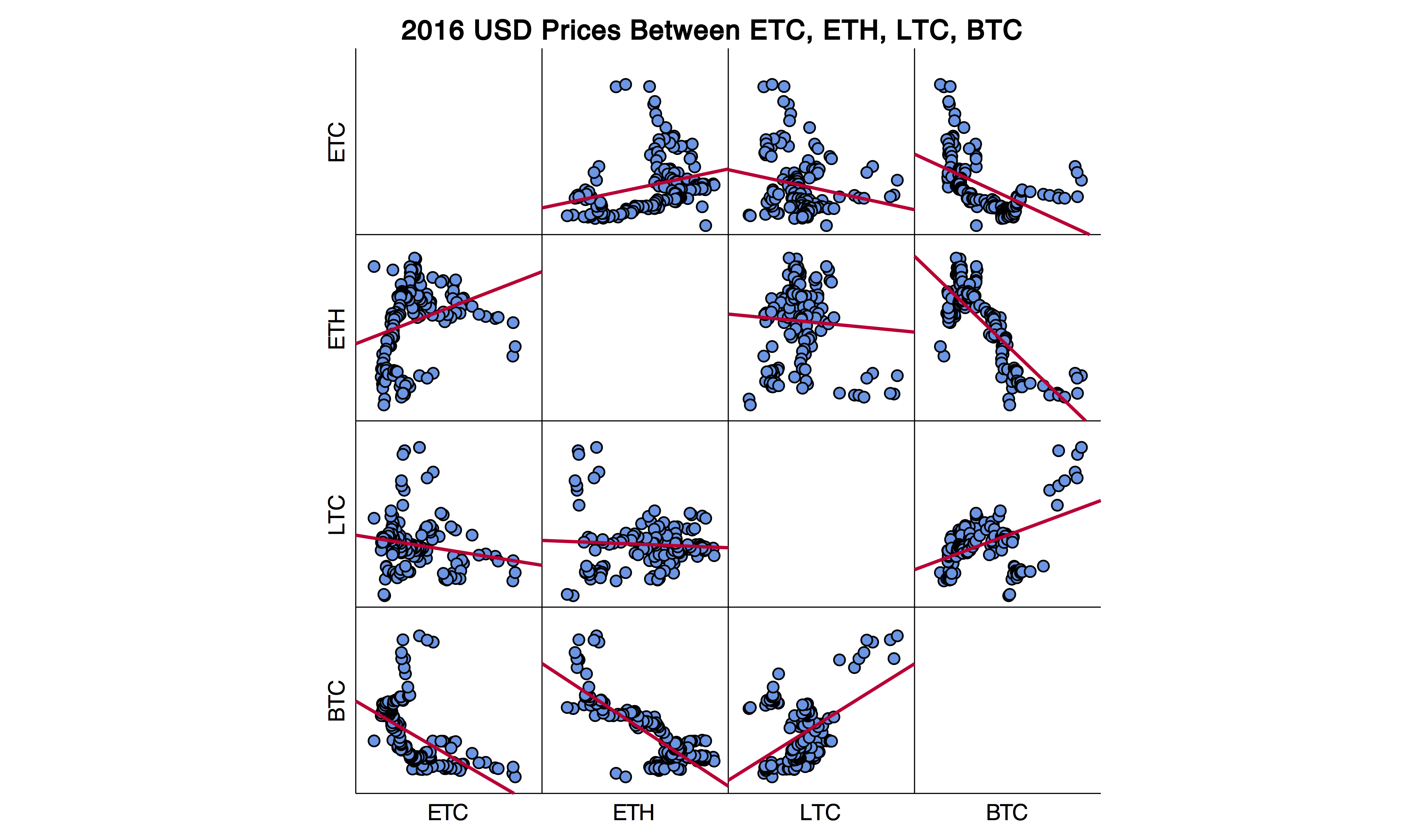
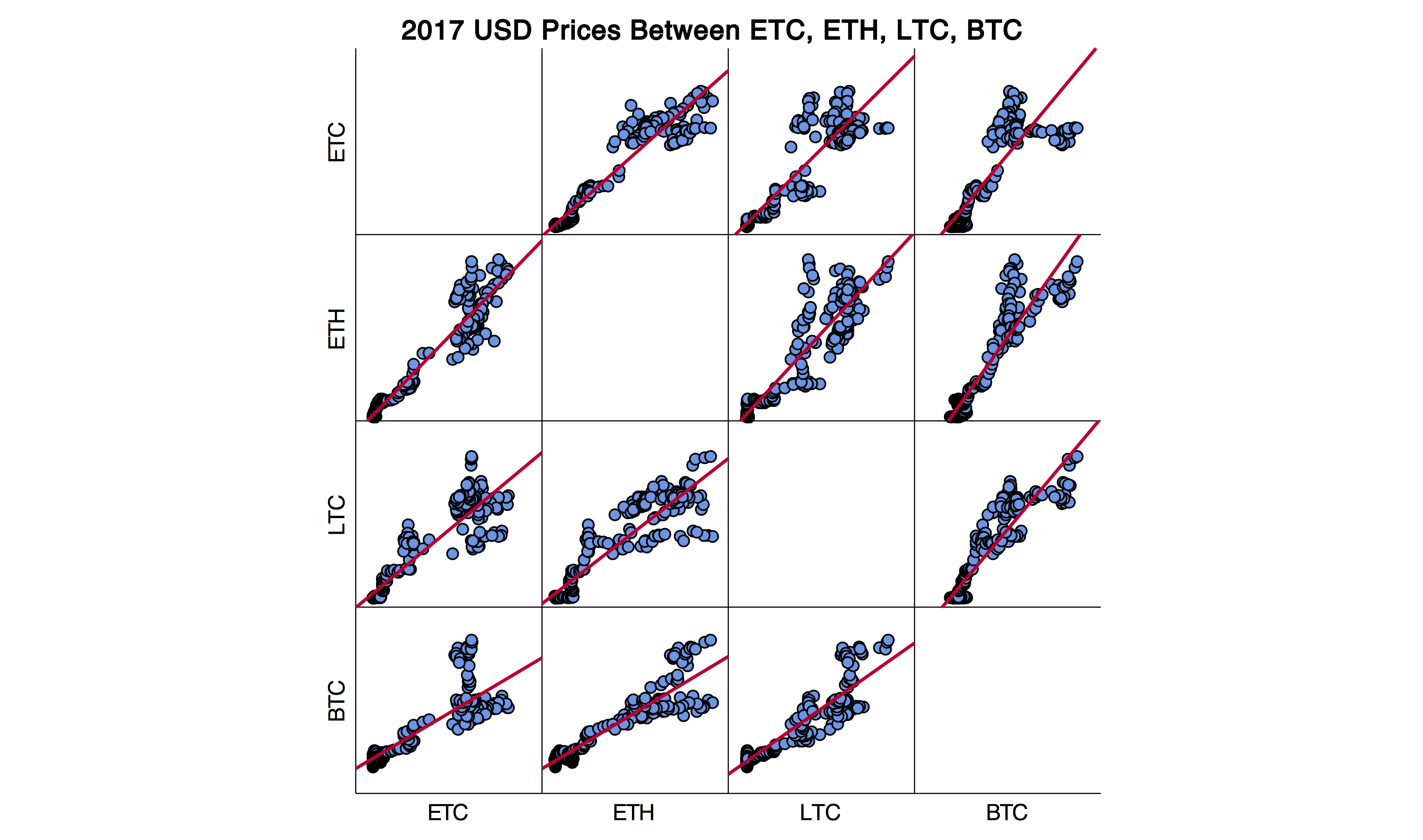
These graphs show the correlation between these four cryptocurrencys are scattered in 2016, but strongly correlated in 2017.
In order to get more details about these correlations, I decided to use our Bayesian Inference Pearson Correlation function to characterize the posterior distribution of the linear correlation between Bitcoin and Etherium, the two highest traded cryptocurrencies by volume. I performed this test twice for 2016 prices then 2017 prices. I kept all options as the default, including a uniform prior (shown by the flat red lines in the below charts). Prior selection is very important for Bayesian analysis, but here I benefit from a large sample size and do not involve more prior information.
[caption id="attachment_7005" align="alignnone" width="4188"]
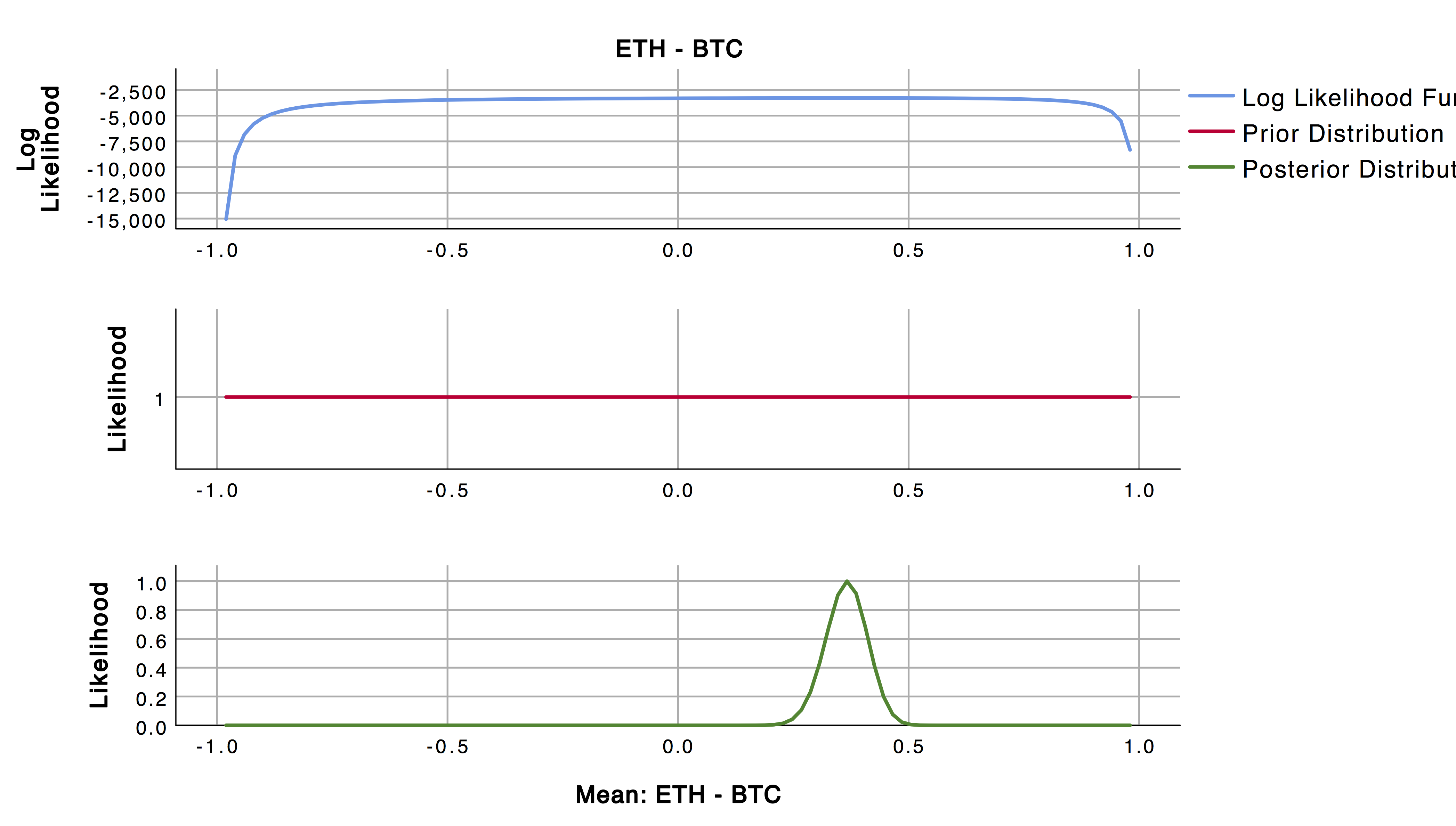
Correlation between ETH and BTC prices in 2016[/caption]
[caption id="attachment_7006" align="alignnone" width="4201"]
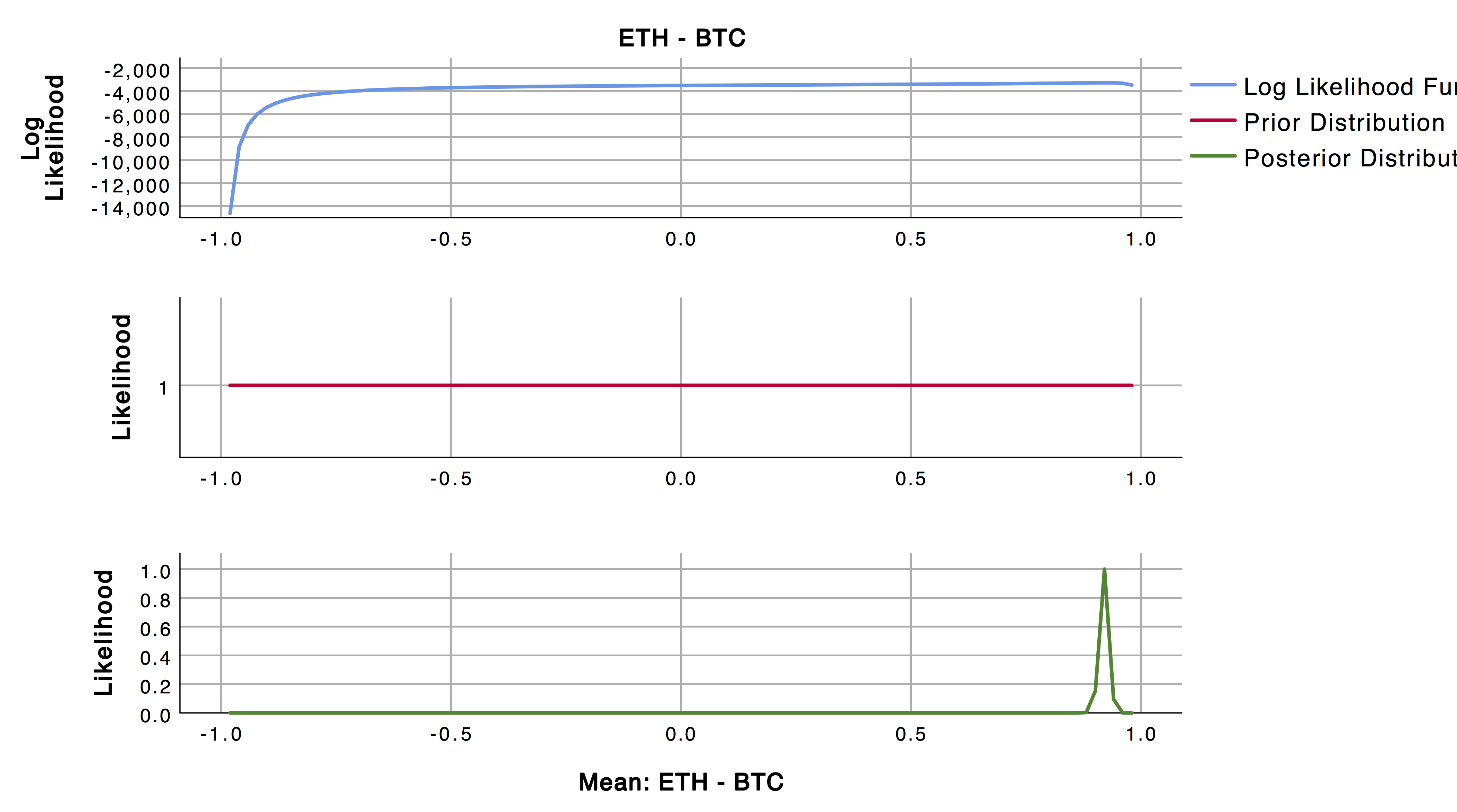
Correlation between ETH and BTC prices in 2017[/caption]
The 95% credible interval of Pearson correlation coefficient for 2016 is (0.274 to 0.452) and for 2017 is (0.901 to 0.940). So, the prices between these cryptos had a low correlation in 2016 but a very high positive correlation in 2017, likely due to the rise of crypto hedge funds. It is interesting to see how these correlations differ between the years, but this example also served as a nice reminder that in Bayesian statistics correlations are not single numbers but rather distributions.
#bayesian#bitcoin#datavisualization#SPSS#SPSSStatistics#statistics#Usecases