Hi,

 

at

 

https://www.ibm.com/developerworks/community/forums/html/topic?id=e8342572-6dc5-4885-ae55-e154e8d37773&ps=25

 

 

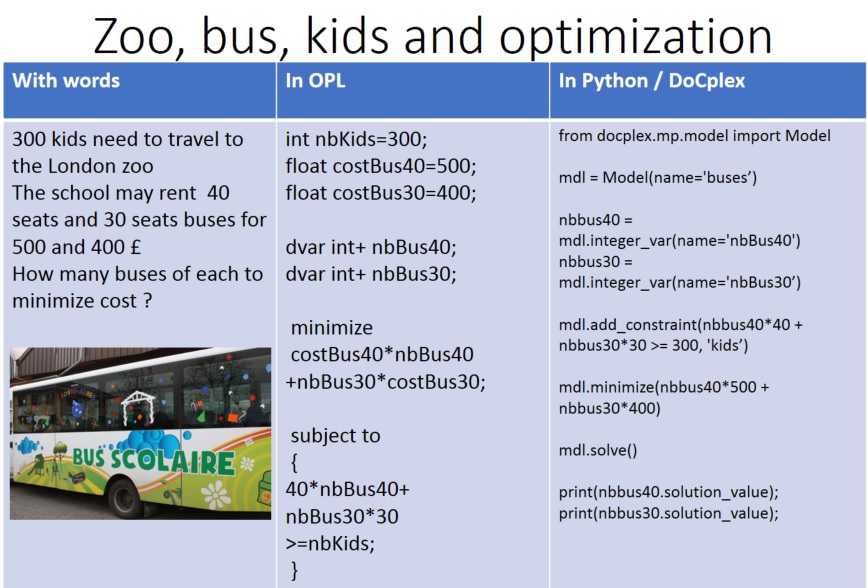
we handled what if analysis and dealt with many options with regards to the number of kids we need to bring to the zoo.

Suppose we need to hedge against uncertainty and make sure that whatever scenario, we have enough buses.

Then we deal with non probabilistic robust optimization, worst case optimization.

And we can write

int nbKids=300;

{int} nbKidsOptions={nbKids+i*10 | i in -10..2};

float costBus40=500;
float costBus30=400;
 
dvar int+ nbBus40;
dvar int+ nbBus30;
 
minimize
 costBus40*nbBus40  +nbBus30*costBus30;
 
subject to
{
 ctKids:40*nbBus40+nbBus30*30>=max(k in nbKidsOptions) k;
}

execute
{
writeln("nbBus40 = ",nbBus40);
writeln("nbBus30 = ",nbBus30);
}

which gives

 

// solution (optimal) with objective 4000

nbBus40 = 8
nbBus30 = 0

This is far from being subtle. We hedge against the worst case. And we already got this for stochastic optimization at https://www.ibm.com/developerworks/community/forums/html/topic?id=7ce856ee-be78-4258-aede-fd9c4c9e464c&ps=25 when we do not use recourse variables.

 

Often, we tend not to hedge against the worst case but instead make sure that in more than alpha % probability everything is fine.

And then with alpha=80% we can write

int nbKids=300;

{int} nbKidsScenarii={nbKids+i*10 | i in -10..2};
float proba[nbKidsScenarii]=[ 1, 1, 2, 2, 2 ,3 ,3 ,4,  5 ,10 ,50 ,10, 7];

assert sum(s in nbKidsScenarii) proba[s]==100; // total probability is 100

float costBus40=500;
float costBus30=400;

int alpha=80; // We want the constraint to be ok with probability 0.95

// number of buses booked in advance
dvar int+ nbBus40;
dvar int+ nbBus30;
// number of buses booked at the last minute which is far more expensive

 
minimize
 costBus40*nbBus40  +nbBus30*costBus30;
 
subject to
{
 ctKids:alpha<=sum(nbKids in nbKidsScenarii)
   (40*nbBus40+nbBus30*30>=nbKids)*proba[nbKids];
}

execute
{
writeln("nbBus40 = ",nbBus40);
writeln("nbBus30 = ",nbBus30);
}

and then we get

 

// solution (optimal) with objective 3800
nbBus40 = 6
nbBus30 = 2

Which means that if we allow the risk to be 20% we move the cost from 4000 to 3800. Quite interesting sometimes.

 

Regards

 

NB: We call ctKids a probabilistic constraint

 

 

#DecisionOptimization
#OPLusingCPLEXOptimizer