Regression is the process of predicting a continuous value. We can use regression methods to predict a continuous value, such as CO2 emission from a car model, using some other variables.
For example, let us assume that we have access to a dataset that contains data related to the CO2 emissions from different cars. The dataset contains attributes such as car engine size, number of cylinders, fuel consumption and CO2 emission from various automobile models. Let us assume that the dataset contains historical data from different cars. Now, we are interested in estimating the approximate CO2 emission from a new car model after its production. This is possible using a machine learning regression model.
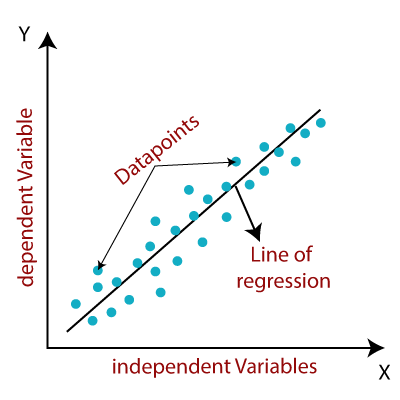
In regression, there are two types of variables: a dependent variable and one or more independent variables. The dependent variable is the "state", "target" or "final goal" we study and try to predict, and the independent variables, also known as explanatory variables, are the "causes" of those "states". The independent variables are shown conventionally by X, and the dependent variable is denoted by Y. A regression model relates Y, or the dependent variable, to a function of X, i.e., the independent variables. The key point in regression is that the dependent variable value should be continuous, and not a discrete value. However, the independent variable or variables can be measured on either a categorical or continuous measurement scale.
So, in our hypothetical example of estimating the approximate CO2 emission from a new car model after its production, we can use the historical data of some cars, using one or more of their features, to make a machine learning model. We can use regression to build such a regression/estimation model. The model can then be used to predict the expected CO2 emission for a new or unknown car model.
Basically, there are 2 types of regression models: simple regression and multiple regression. Simple regression is when one independent variable is used to estimate a dependent variable. It can be either linear on non-linear. For example, predicting CO2 emission using the variable ‘Engine Size of a Car’. The linearity of regression is based on the nature of the relationship between independent and dependent variables.
When more than one independent variable is present, the process is called multiple linear regression. For example, predicting CO2 emission using the variables ‘Engine Size of a Car’ and ‘the number of cylinders present in a car’. Again, depending on the relationship between dependent and independent variables, multiple linear regression can be either linear or non-linear regression.
Let us now examine some sample real-world applications of regression. Essentially, we use regression when we want to estimate a continuous value.
- One of the applications of regression analysis could be in the area of sales forecasting. We can try to predict a salesperson's total yearly sales from independent variables such as age, education, and years of experience in the sales profession.
- Regression analysis can also be used in the field of psychology, for example, in order to determine individual satisfaction, based on demographic and psychological factors.
- We can use regression analysis to predict the price of a house in an area, based on its size, number of bedrooms, and so on.
- We can even use regression analysis to predict employment income for independent variables, such as hours of work, education, occupation, sex, age, years of experience, and so on.
We can find many examples of the usefulness of regression analysis in many other fields or domains, such as finance, healthcare, retail, and more.
We have many regression algorithms. Each of them has their own importance and a specific condition to which their application is best suited.
 *************************************************************************************
*************************************************************************************
The author of the technical article, Subhasish Sarkar, is an IBM Z Champion for 2020.
******************************************************************************************************************