Hi Walker,
To expand on Jon's (correct) suggestion to check the algorithms, the four types of sums of squares (SS) used in the SPSS Statistics GLM and UNIANOVA procedures are based on the definitions given by SAS. Type I SS are dependent upon the order in which terms are entered into the model, and for models with terms specified in appropriate order, are equivalent to what are sometimes called sequential SS, as they can be calculated by comparing the residual or error SS from sequentially more complex models as individual terms are added. These are the SS given in the R anova class in the stats package.
Type II, III, and IV SS are designed to be independent of the order of specification of model terms, and involve the notion of
containment of effects. Specifically, Effect F
1 is contained in Effect F
2 if:
- Both involve the same covariate effects, if any.
- Any factors in Effect F1 are a proper subset of those in Effect F2 (i.e., all factors appearing in Effect F1 also appear in Effect F2, and Effect F2 involves at least one more factor).
Note that the intercept or constant is contained in all effects involving only factors, but not in any effect involving covariates, and no effects are contained in the intercept.
The Anova class in R's car package uses the terms Type II and Type III (or 2 and 3), but the definitions are not identical to the way SAS has defined them. From the first paragraph of the Details section of
https://rdrr.io/cran/car/man/Anova.html: "The designations "type-II" and "type-III" are borrowed from SAS, but the definitions used here do not correspond precisely to those employed by SAS. Type-II tests are calculated according to the principle of marginality, testing each term after all others, except ignoring the term's higher-order relatives; so-called type-III tests violate marginality, testing each term in the model after all of the others. This definition of Type-II tests corresponds to the tests produced by SAS for analysis-of-variance models, where all of the predictors are factors, but not more generally (i.e., when there are quantitative predictors)."
Since your specified model doesn't involve any factors, there are no containment relationships in the model. In these circumstances, Type II and Type III sums of squares as defined by SAS and in SPSS Statistics are the same. If you were looking at a model with all categorical predictors (what SPSS Statistics usually calls factors), then the Type II sums of squares should match those you get with R's Anova class from the car package. You should also get matching results regardless of the types of predictors if the model doesn't involve any product or interaction variables (in which case Type II and Type III SS would be the same in R as well).
The difference in the two approaches is that the SAS approach relies on containment to determine which effects in the model are to be adjusted for when calculating sums of squares for a particular effect, while R relies on the
marginality principle mentioned in the quote from the R car documentation. Containment is defined above, and is essentially arithmetic in nature, while marginality is based more thoroughly on theoretical principles.
SAS PROC GLM and SPSS Statistics GLM/UNIANOVA use what's known as a non-full rank or canonical overparameterized representation of models with categorical factors as predictors. This involves an indicator column for each level of each factor, with product and nested terms constructed from these columns. This is in keeping with the fundamental nature of the model, which has more parameters than means with which to estimate population parameters. It results in redundant or linearly dependent columns in the model design or X matrix whenever you have at least one factor with an intercept, or at least two factors, with or without an intercept. Many linear and generalized linear models programs or procedures handle this fundamental overparameterization by reparameterizing the model to full rank via the use of contrast codings for factors. SAS and SPSS Statistics GLM procedures maintain the canonical overparameterized representation, and handle redundant parameters by aliasing them to 0 in the process of sweeping the X'X matrix during estimation. This is why you'll usually see parameter estimates with 0 values and missing values for standard errors and other statistics in models with factors. Hypothesis tests are conducted by constructing what are referred to as L matrices or linear combinations of the model parameters, and these L matrices (which will be single row vectors for single degree of freedom (df) tests) are used to calculate the SS for model terms based on the model specifications, the defined type of SS, and the available data.
When using this canonical overparameterized representation, if an effect is contained in another effect, then removing the contained effect from the model specification will not change the overall model fitted, and one can't calculate sums of squares for that effect by fitting the model without it and comparing the residual SS to that from the full model, as the two are the same overall model and have the same residual SS. For example, if you have a factorial model with factors A and B, and you fit the terms in any order where A*B (A:B in R's notation, or the A by B interaction effect) precedes any other effects, the full model SS are accounted for at that point and any additional reduction in residual SS is null, so the Type I SS for terms following A*B would be 0 (and would be associated with 0 df). More fundamentally, it's not possible to construct an hypothesis test of just the parameters in the contained effect.
SAS's Types II, III, and IV SS are designed to be independent of the order in which terms are specified in the model, and to provide what some consider reasonable ways to deal with the implications of containment. Type II SS are equivalent to collecting results from calculating Type I SS from multiple fittings of the same model with terms fitted in different orders where necessary to give reductions in residual SS for each term entered after all other terms that do not contain that term. Type III SS are designed to test hypotheses about contained terms that distribute containing effects evenly across the levels of the contained effects, making the hypotheses tested supposedly the same as would be tested with completely balanced data. Type IV SS try to extend this approach to models involving empty cell combinations of factors.
As noted, containment is a mathematical relationship, while marginality is more theoretical. The marginality principle says that it doesn't make sense to estimate or test effects that are marginal to higher-order terms of which they are a part, or to remove the marginal effects from the model as long as the effects to which they're marginal remain in the model. So if you have A*B (A:B in R) in a model, then testing A or B is not meaningful or appropriate, because the interaction implies that there isn't a single main effect of A or B, only effects fixing at levels of the other effect. This applies both to factors, where marginality leads to containment, but also to covariates, where it typically does not. That is, if you have covariates X and Z as predictors, and you also have their product or interaction term, then interpreting "main effect" slopes makes no sense, since the model implies that the slopes depend on the location on the other predictor, as is the case with factors, even if it doesn't lead to the same containment relations as with factors.
So in SAS and SPSS Statistics, using the SAS definitions, if you have covariates and their interactions, since there are no containment relationships involved, Type II and III SS are the same, computable by comparing the change in residual SS from removing one term at a time from the overall model. The Type II SS in Anova in R, which bases things on the marginality principle, calculates SS for the highest order terms (those not marginal to others in the model) the same way, but lower order marginal terms are calculated by comparing changes in residual SS from removing that term from a model that contains only the other terms in the overall model to which that term is not marginal. So in a case like yours, with just three covariates and all their product terms, each main effect SS is calculated by adding a covariate to a model containing only the other two main effects and their interaction, or equivalently, removing it from a model with the other two main effects and their interaction, because these other two main effects and their interaction are the only terms in the full model to which this main effect is not marginal. For the two-way interaction terms, which are marginal only to the three-way term, each can be removed from the complete (one and) two-way model, or added to the model containing all other main effects and two-way terms. The three-way term is calculated by comparing the complete model to the model with all two-way terms.
If you want the exact same test results in SPSS Statistics as are shown in the R Anova Type II table, it's possible to get them, but not with a single invocation of a procedure, and thus not in a single table. Running models with subsets of the terms in your full model with the default Type III SS will give matching effect SS for appropriate terms, but will also change the error term and df, so a syntax-only option based on use of the TEST subcommand would be needed.
I'm going to use x1, x2, and x3 as covariates predicting the dependent variable y in the following example commands. You can adapt these to your particular variable names by substituting those names everywhere those generic names appear. Also not on the TEST subcommands that I'm specifying SSE and DFE, which you would replace by the appropriate numbers (7.7665 and 106, respectively, for this example).
As noted above, the three-way term's test is the same with Type II or III SS, so you've already got that result, and in a new problem it would also appear when running the complete model. To get results for the two-way terms, you would need only one additional model to be run, but would need three TEST subcommands to use the original error term, as follows:
UNIANOVA y WITH x1 x2 x3
/DESIGN=x1 x2 x3 x1*x2 x1*x3 x2*x3
/TEST x1*x2 VS SSE DF(DFE)
/TEST x1*x3 VS SSE DF(DFE)
/TEST x2*x3 VS SSE DF(DFE).
For the main-effects terms, you'd have to run a separate model for each one:
UNIANOVA y WITH x1 x2 x3
/DESIGN=x1 x2 x3 x2*x3
/TEST x1 VS SSE DF(DFE).
UNIANOVA y WITH x1 x2 x3
/DESIGN=x1 x2 x3 x1*x3
/TEST x2 VS SSE DF(DFE).
UNIANOVA y WITH x1 x2 x3
/DESIGN=x1 x2 x3 x1*x2
/TEST x3 VS SSE DF(DFE).
The results from the TEST subcommands are shown in output sections labeled "Custom Hypothesis Tests." The labeling isn't optimal (the term is just labeled as "Contrast" in the ANOVA table), and when you have more than one of these you have to look at the Index above the tables to see the hypotheses, but the results are there.
Hope this helps.
------------------------------
David Nichols
IBM
------------------------------
Original Message:
Sent: Mon December 28, 2020 03:26 PM
From: Jon Peck
Subject: GLM Type II & Type III give same result
Appendix H in the Algorithms document spells out the Type II and Type III calculations (and Type I and Type IV). Note that under some circumstances, Type II and Type III sums of squares will be the same.
--
Original Message:
Sent: 12/23/2020 4:14:00 PM
From: Walker Pedersen
Subject: GLM Type II & Type III give same result
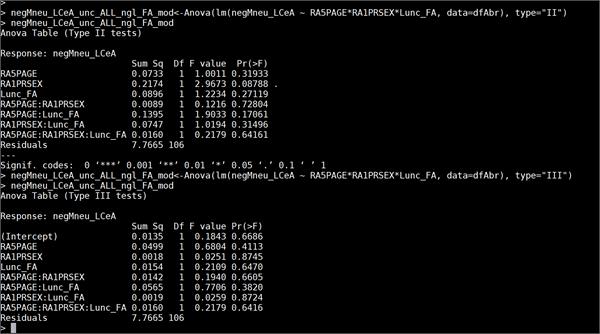
When running a univariate GLM with several interaction terms, I am getting the same values when using Type-2 and Type-3 sum of squares (see attached image). If I run the same analysis in R, the Type-3 sum of squares looks the same as the SPSS output, but the Type-2 sum of squares is different. Since the model has interaction terms, I would expect Type-2 SS to be different than Type-3. This makes me suspect that SPSS isn't implementing Type-2 SS correctly, is this possible?

#SPSSStatistics